為學日增 為道日損~ Sign in Recent Site Activity Report Abuse Print Page Powered By Google Sites Recent Site Activity Report Abuse Print Page Powered By Google SitesNov 27, 15 · (1)x=60° (2)x=1° y=40 ° (3)x=30 ° y=100°正しいでしょうか?BIGLOBEなんでも相談室は、みんなの「相談(質問)」と「答え(回答)」をつなげ、疑問や悩みを解決できるQ&Aコミュニティサイトです。あなたの相談(質問)にみんなが回答をしてくれるため、疑問や悩みをすばやく解決することOct 23, 18 · 今回は外心について学習しましょう。外心は図形を扱った問題では頻出です。外心のもつ性質やそれに関わる公式などを使いこなせるようにしておきましょう。 なお、記事の画像が見辛いときはクリックすると拡大できま

高校数学a 三角形の外心2 実践 練習編 映像授業のtry It トライイット
外心 問題 解き方
外心 問題 解き方-数学a 授業プリント# 27 年 組 号 氏名 三角形の重心 b c a n m l g ☆ ☆ 2 2 1 1 2 1 㾻三角形の3 つの中線は、1 点で交わる。 この点 を重心という 㾼重心は、各中線を2 1 に内分する 例題1 右の三角形で点g は4abc の重心である。 このときbl、cg の長さを求めなさい。 b c a n m l g 3 cm傍心で解ける問題は、垂線や外心で 解ける問題も多くあるみたいです。 この問題(40,,50,80)は、 abcの外心o をとると、 四角形aocdは円に内接する 四角形になって解決します。 ラングレーのページの「問題13」を


数学难题 与三角形 圆 内心 外心有关的题 在三角形abc中 角a的平分线ad交三角形abc的外接圆于e O是外心 Ae的中点i为三角形abc的内心 求证oi是三角形ibd外接圆的切线 作业 慧海网
外心の角度の関係 その1 ABCの外心Oをとして、外心O が ABCの内部にあるとき、外 接円の半径から、3つの二等辺 三角形がある。その底角を図の ようにa,b,c,とすると、 2a+2b+2c=180° 2でわっ三角形の5心(外心・内心・重心・傍心・垂心)のうち外心について考えていきます。 三角形の各辺の垂直二等分線は 1 点で交わります 。 これは以下のように証明ができます。 において,辺 , の垂直二等分線の交点を とします。 は の 垂直二等分線上の点なので, ①④ 外心と重心の距離 ⑤ 垂心と重心の距離 (ⅰ)外心と重心と垂心は一直線上にある. この3点がのっている直線はオイラー線と呼ばれ る.ではまず,そのことを証明しておこう. 図において,o を abc の外心,h を垂心,g
三角形の外心の求め方・性質 三角形のそれぞれの辺から垂直二等分線を引きます。すると その垂直二等分線は必ず1か所で交わります 。 その交わってできた唯一の点が 外心 です。 外心はoと表すことが多いです。 こういう外心の問題が出てくるときって大概左上のような三角形の図形だけしたがって、外心は外接円の中心であることが分かりました。 おわりに 今回は五心の中から 「外心」 をピックアップして解説しました。 外心の性質はすでに知っているものとして、問題が出されるので、しっかりと覚えておくようにしましょう。三角形の外心、三角形の外接円 この1点で交わった点 o を三角形の外心という。 外心 o を中心として、半径 oa の円が三角形 abc の外接円である。 oa=ob=oc ol⊥bc 、 om⊥ac 、 on⊥ab
問題 次の図で、\(\triangle {\rm ABC}\) とその外心 \({\rm O}\) について、\(\angle{\rm A}=80^\circ\) のとき、次の角を求めよ。問題自体はシンプルですが, かなりの難問です まず, 結ぶ線が特殊ですね 点\(e,f\)を結ぶのは考えづらいし, ましてや外心と傍心を結ぶなんてやばそうです 僕は, この問題が難しいとうわさで聞いていたので解こうとしたのですが全然わかりませんでしたMar 06, 21 · 三角形の五心は有名ですが非常に豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出です。三角形の五心の定義と重要な性質をまとめておきます。



初中數學 藉助一道和垂心 外心有關的題目複習下三角形的 心 每日頭條


Studydoctor三角形の外心 高校数学a Studydoctor
三角形の内心・外心・重心に関するやさしい問題 ~前期日程大分大学経済学部の入試問題 18年08月25日 数学・数学教育 18年8月25日(土)TLT \ t g w elearning Ȋw G Newton m ł H Newton ̊֘A Ђ č œ 擾 TLT \ t g B Z ^ ܂ ̃ C i b v円の五心の基礎ついてまとめました‼ 学年 中学3年生, 単元 円周角の定理(円周角と中心角),円周角の定理の利用, キーワード 垂心,円,外心,内心,円周角



与三角形 外心 牵手的向量问题研究 参考网
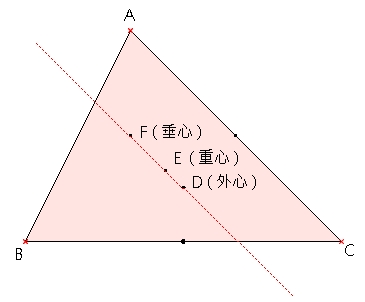


挑戰scienceword實做數學原理 尤拉線euler Line 含試用心得募集活動
外心、内心の基本問題(角度) abcの外心をoとする。角α、βを求めよ。 α β 51° 19° o 答α=70°, β=° o β α 26° 40° 答α=100°, β=24° o α β 41° 18° 答α=59°, β=118° o α β 68° 24° 答α=44°, β=136° o 36° α 答α=54° α 30° 21° 答α=102° abcの内心をiとする。角α、βを求めよ。「外心」をヒントにして解く問題だね。 外心 とは、 外接円の中心 のこと。外接円の中心だからこそわかる、次の2つの特徴をしっかりおさえておこう。外心の性質を用いた応用問題3選 ここからは、外心の性質を用いた応用問題について見ていきましょう。 具体的には、 角度を求める問題;



与三角形 外心 牵手的向量问题研究 参考网



1 外心的定義 三邊中垂線之交點 Lalalala
Gc_'htm gc_ 蜂須賀優佑 図形htm gc_equi_tri2a_0htm gc_外心htm gc_gaisinntosuisinnhtm;Gc_外心と垂心htm gc_htm gc_藤村 接弦定理htm gc_よっこたhtm gc_かはたhtm;この問題が、体積を答えさせるだけの問題として、 高校入試で出るとは考えにくいです。 なぜなら、\(1\) 辺が \(acm\) の正四面体の体積は \(\displaystyle \frac{\sqrt{2}}{12}a^3(cm^3)\) という事実を暗記してきた生徒に対して無力な問題だからです。 しかし、


立体几何中三角形的四心问题 内心



三角形的外心1 Youtube
Q 外心をo 内心をiとする。oiを求めよ ab=8 bc=7 ca=5の三角形があり、外心をo 内心をiとする。oiを求めよ。 という問題の解説をどなたかお願いします。 オイラーの定理を使えば簡単なのですが 数iAの問題として出ていたので問題 空間内に四面体abcdを考える。このとき、4つの頂点 a , b , c , d を同時に通る球面が存在することを示せ。イズミの解答外心,重心,垂心は1直線上にあることを示すことができる.(内心は,これら3点と同一直線上にあるとは限らない) (51)を直接示そうとすると, の 差 を比較することになるが,これらはすでに複雑な三角関数の分数式になっているので,通分などが容易


这个 三点共线 问题的证明很巧妙 中垂线


数学中直线和不等式的结合问题是什么 看看今天的数学题目 竞赛网 中国名校19年五大学科竞赛门户网站
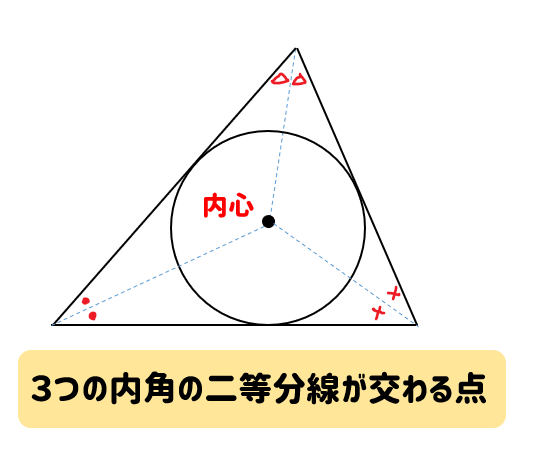
三角形の外心の性質 三角形の3つの辺それぞれの垂直二等分線は、1点で交わる。この点のことを三角形の外心という。 このテキストでは、この定理を証明します。 証明 ABCにおいて、辺ABの垂直二等分線と、辺ACの垂直二等分線の交Aug 09, 07 · 三角形abcの外心をoとしてoは三角形の中にある。このとき 「(2*→ao)*(→ab)=(→ao')*(→ab)=ab^2」がいえる。ただしo'はaoの延長でao=ao'となる点である。またabにobiglobeなんでも相談室は、みんなの「相談(質問)」と「答え(回答)」をつなげ、疑問や悩みを解決できるQ&Aコミュニティサイトです。外心 三角形の3辺の垂直二等分線は1点で交わる。この点を外心という。 外心は3つの頂点から等距離にある。(外接円の中心) 内心 三角形の3つの内角の二等分線は1点で交わる。この点を内心という。 内心は3つの辺から等距離にある。(内接円の中心) 重心
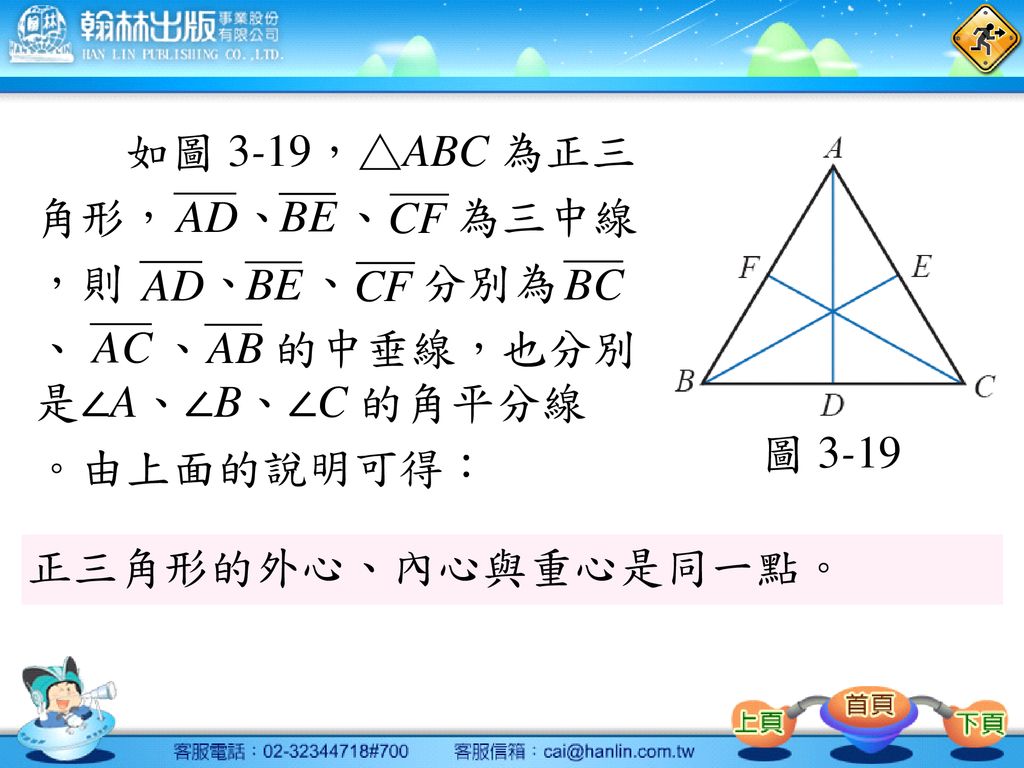


三角形的外心三角形的內心三角形的重心自我評量 Ppt Download



初中數學 藉助一道和垂心 外心有關的題目複習下三角形的 心 每日頭條
位置ベクトルを求める問題(数学b) この $3$ つが挙げられます。Jul 26, 17 · 垂直二等分線 三角形の外心の話をする前に、垂直二等分線についておさらいをしておきましょう。 線分 AB があったとき、 AB の中点を通り、 AB と垂直に交わる線のことを、線分 AB の垂直二等分線(perpendicular bisector) といいます。 上の図で、線分 AB の中点を M としたとき、直線 PM が垂直二等分三角形の外心 図の ABCをみてください。 ABCの3つの頂点を通る円を一緒に描いてありますが、この円のことを外接円と呼びます。三角形の周りを囲っている円ですね。 この外接円の中心の点を ABCの外心と呼びます。 この外心は、 ABCの各辺の
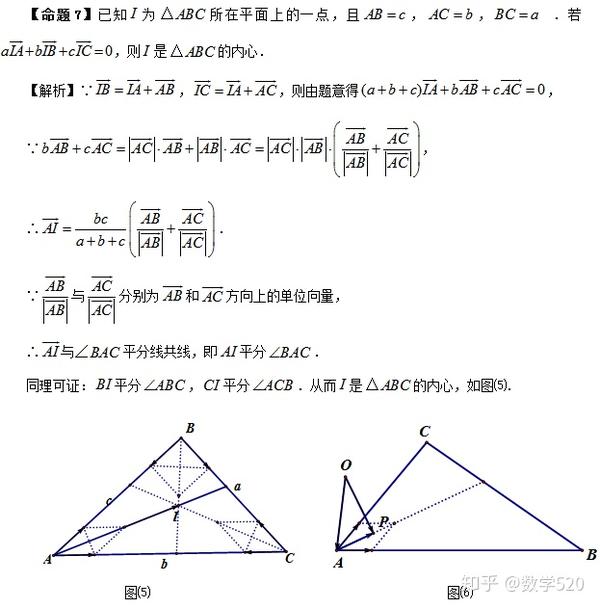


高中数学 平面向量中的三角形 四心 结论 知乎



初三数学第1讲 三角形 提高班 教师版下载 Word模板 爱问共享资料
重要な相互関係 1 正三角形のときは,重心・外心・内心・垂心は一致します. 2 三角形の外接円の半径Rは,内接円の半径rよりも大きくなります.(2倍以上になります.)数学授業プリント(高校) 21年2月11日 プリントを1枚追加 21年2月6日 プリントを1枚追加, 年12月13日 プリントを2枚追加, 11月28日 プリントを1枚追加, 11月14日 プリントを3枚追加, 8月9日 プリントを1枚追加, 5月31日 プリントを4枚追加, 1月11日 チェバ/メネラウス定理プリントを数学A問題 内接円と傍接円 ⊿abc が与えられている ⊿abc の内接円と、辺 bc, ca, ab との 各々の接点を d, e, f とおく ⊿abc の傍接円と、辺 bc, ca, ab (延長)との 各々の接点を l m,n とおく d から ef に下ろした接線の足を h とし l から mn に下ろした接線の足を k とする


建议收藏 年清华大学强基计划数学试卷及答案解析 教育资讯 八戒游戏
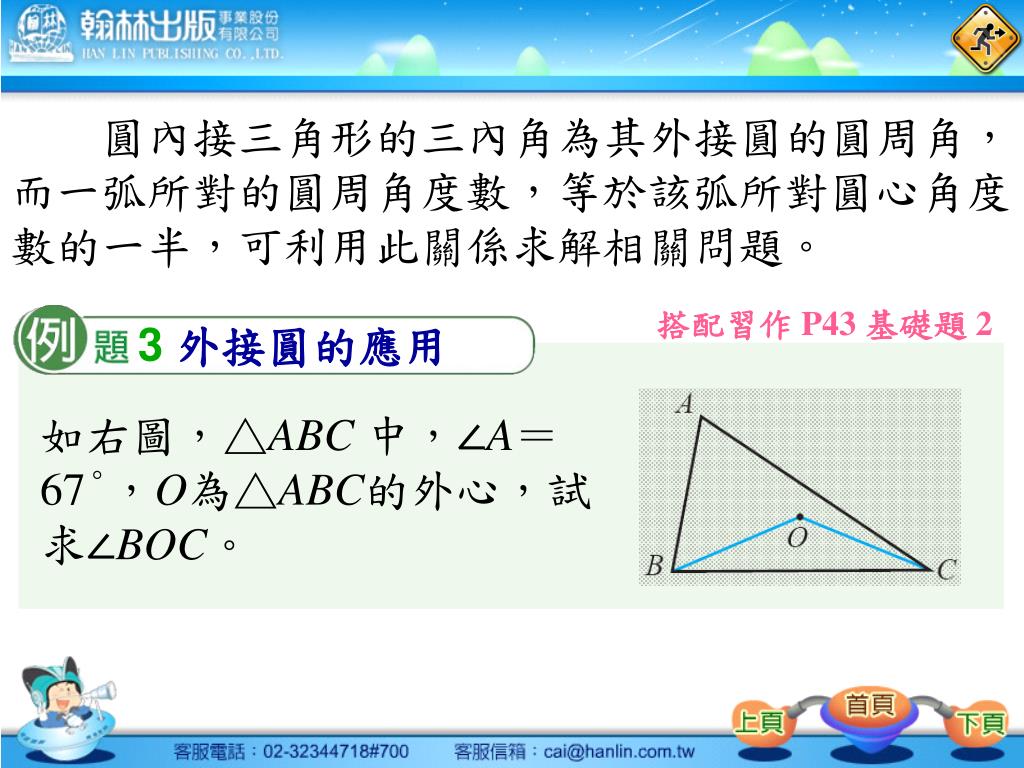


Ppt 三角形的外心powerpoint Presentation Free Download Id



Jimmy 三角形的四心内心垂心外心重心



三角形的外心定義 Tom123



中纪委发文 严查医药腐败 凤凰网健康 凤凰网



点与圆的位置关系下载 Word模板 爱问共享资料
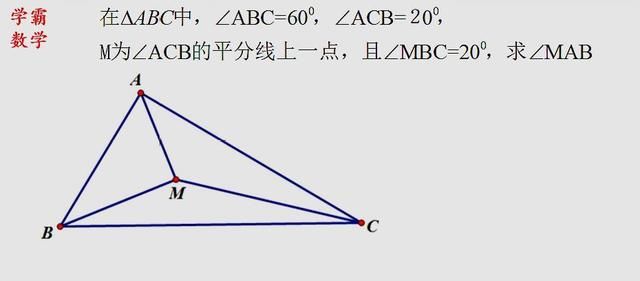


等腰三角形的内心和外心



数学 三角形の外心の解き方が分かりません 高校数学に関する質問 勉強質問サイト


确定圆的条件 圆ppt教学课件 第一ppt



高校数学a 三角形の外心2 実践 練習編 映像授業のtry It トライイット


玉數臨風 九上8 三角形的外心



Days To Go 1 Days 四心提提你 數學補習 Dse補數學 中學數學專科補習社
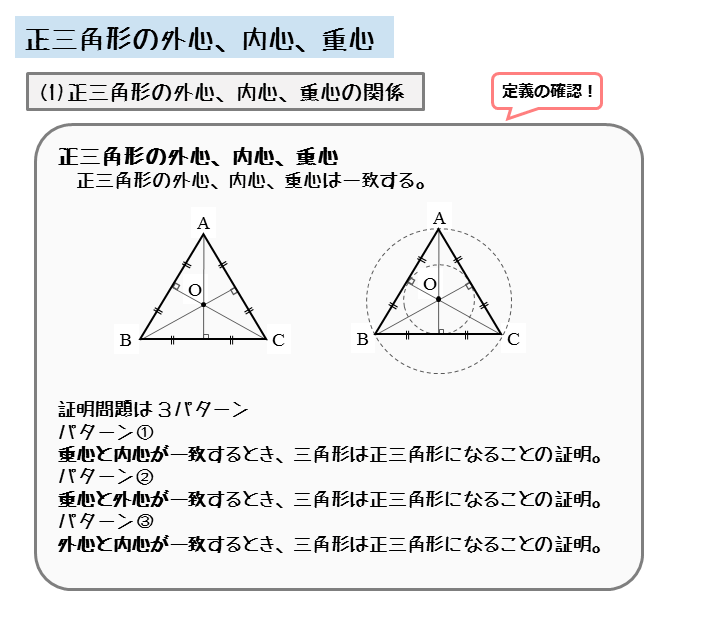


図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
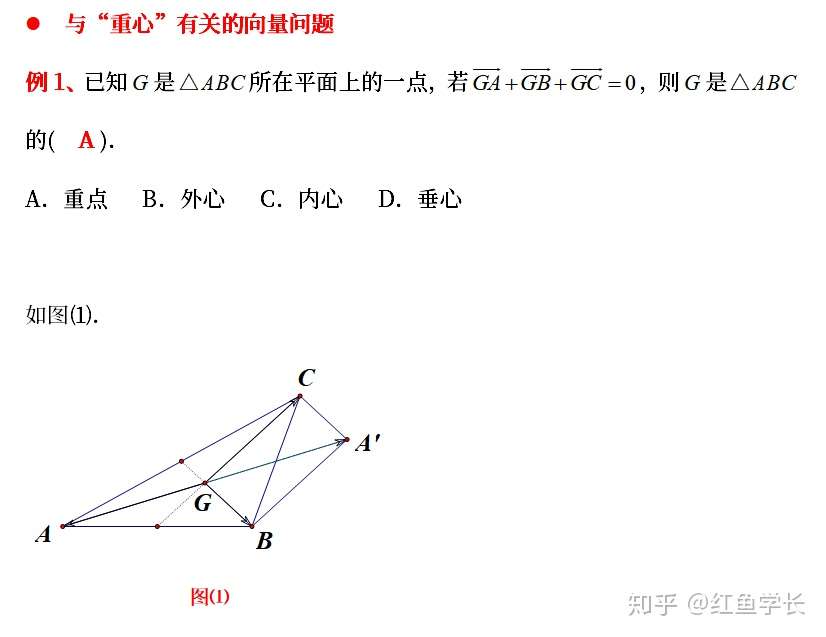


高考有哪些快速解题技巧 奔驰定理 了解一下 选择填空拿满分 知乎



三角形四心的向量性质及证明 百度文库



三角形的外心定義 Tom123



三角形の外心について知っておきたい知識まとめ 理系ラボ
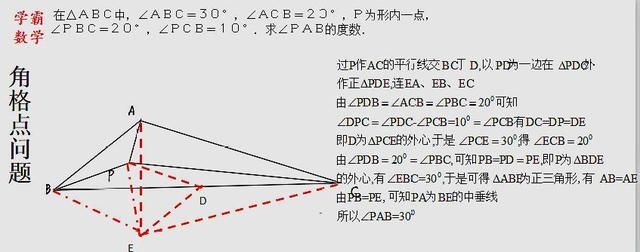


等腰三角形的内心和外心


数学难题 与三角形 圆 内心 外心有关的题 在三角形abc中 角a的平分线ad交三角形abc的外接圆于e O是外心 Ae的中点i为三角形abc的内心 求证oi是三角形ibd外接圆的切线 作业 慧海网


高考命題重點和熱點 平面向量問題 垂心外心合力解題 愛經驗


外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ



当中线遇上球 1分必看 19年全国1卷理科数学12题解析 简书



8种方法解决一道三角形中角格点经典问题 题型虽老 但仍有价值 外接圆 外心 共圆 网易订阅



改訂版 4step数学a P125 2 三角形の外心 内心 重心


三角形 五心 优美的向量形式



李傑老師 回覆高二學生問題 重心 內心 外心 垂心的線性組合熟練嗎 Facebook



觀念 三角形的外心的位置 Youtube


平面几何问题 Geogebra



三角形の外心 定義と性質を証明問題で解説 高校生向け受験応援メディア 受験のミカタ



平面向量重心平面向量中的三角形四心問題重心 垂心 外心 騰訊視頻翻譯此網頁 Rldft



高1数学a平面図形 この問題を教えてください Oは外心a Bの角度を求 数学 教えて Goo


鈍角三角形の外心 思考力を鍛える数学



关注 回复帖子0条回帖 圆锥曲线与四心问题 内心 重心 垂心 外心 浏览9 电脑端 06 27 12 36 近几年圆锥曲线的命题风格看 既注重知识又注重能力 既突出圆锥曲线的本质特征 而现在圆锥曲线中面积 弦长 最值等几乎成为研究的常规问题



高考立体几何中三角形的四心问题 网易订阅


三角形四心问题 腾讯视频



高考立體幾何中三角形的四心問題



三角形の外心 高校数学a Youtube



下の図において 点oは Abcの外心である A Bを求めよ の問題で こ 高校 教えて Goo



Q038的一个性质 超理论坛


三角形四心问题与向量重难点复习 高二秋季b站直播课第一讲 哔哩哔哩 つロ干杯 Bilibili



三角形的外心與外接圓 Geogebra



三角形外心尺规作图 第1页 一起扣扣网


三角形四心问题 腾讯视频



关注 回复帖子0条回帖 精与三角形相关的其他向量问题总结 浏览757 电脑端 19 08 18 08 00 与三角形相关的向量问题总结 三角形的四心是指三角形的重心 外心 内心 垂心 当且仅当三角形是正三角形的时候 重心 垂心 内心 外心四心合一心 称做



企鹅 高中一年级数学 四心 问题 教育 央视网 Cctv Com


三角形内切圆画法图片展示



外心 數學名詞 外心是三角形三條邊的垂直平分線的交點 即外接圓的圓 華人百科


96年自由軟體impress簡報製作比賽九年一貫數學領域九上課程三角形的心 竹南國中林榮耀老師製作 Ppt Download



國中二年級三角形的內心與外心教學目標教學設計學習活動學習評量 Ppt Download



如何找几何体外接球 三人行教育网 Www 3rxing Org
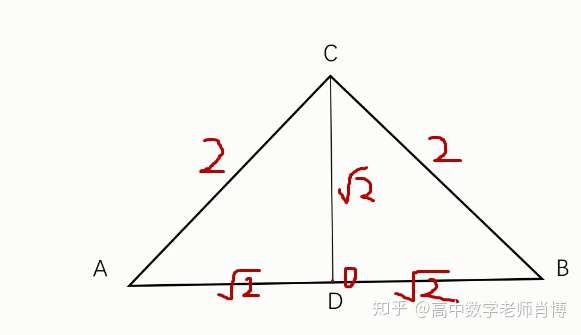


肖博数学 高考数学解题 秒杀向量巨难题型 四心问题 知乎
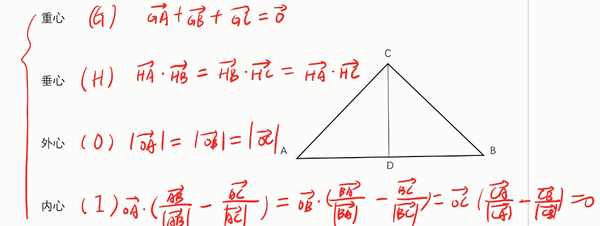


高考数学解题 秒杀向量巨难题型 四心问题 附视频 知乎



三角形外心性质 第1页 一起扣扣网



外心 內心 重心的比較 Youtube


教育雲 教育媒體影音



高校数学a 三角形の外心2 実践 例題編 映像授業のtry It トライイット



关注 回复帖子0条回帖 圆锥曲线与四心问题 内心 重心 垂心 外心 浏览9 电脑端 06 27 12 36 近几年圆锥曲线的命题风格看 既注重知识又注重能力 既突出圆锥曲线的本质特征 而现在圆锥曲线中面积 弦长 最值等几乎成为研究的常规问题



平面向量重心平面向量中的三角形四心問題重心 垂心 外心 騰訊視頻翻譯此網頁 Rldft
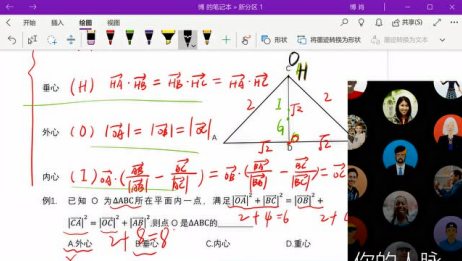


高中数学最难的部分题型平面向量四心问题解题技巧 爱言情



高校数学b 三角形の外心oに関するベクトルの等式 Aoa Bob Coc 0 受験の月
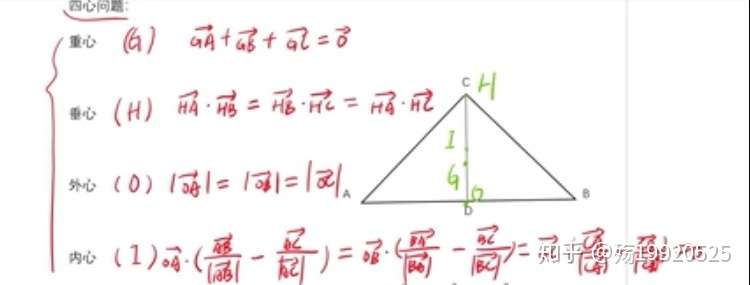


高考数学快速解题法之秒杀向量四心问题 知乎



外心 內心 重心的比較 Youtube



外心垂心問題 Geogebra



向量妙解三角形 四心 参考网



三棱锥外接球直角三角形内心外心 哔哩哔哩 つロ干杯 Bilibili



三角形常用的各心性质 百度文库



外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学塾



高中数学外心内心题目 第1页 一起扣扣网



企鹅 高中一年级数学 第二章解三角形1 1 正弦定理 教育 央视网 Cctv Com



愛學網播放影片


外接円 外心について



推荐 我又回想起了被数理化支配的恐惧 综合讨论 Taptap 社区



外心定义三角形任两边的垂直平分线交点即为外心 精 下载 Word模板 爱问共享资料



外心内心 心内心外 都有装饰你的一片天 哲理文章 三联



Ppt 三角形的外心powerpoint Presentation Free Download Id


Re 問題 數學解答 有問必答 盡量幫忙 場外休憩區哈啦板 巴哈姆特



出道数学题28 最著名三角极值 发布3 1种解法 年10月13日未名空间存档 看帖神器



Jimmy 三角形的四心内心垂心外心重心



三角形内心外心 第1页 一起扣扣网


含有60 的三角形的性质与判定之三 金磊讲几何构型 微信公众号文章阅读 Wemp



8种方法解决一道三角形中角格点经典问题 题型虽老 但仍有价值 外接圆 外心 共圆 网易订阅



0 件のコメント:
コメントを投稿