重心の求め方について その2 (1)高さh,底面の半径rの円錐の場合 (2)半径rの半円球の場合 (3)(1)の円錐と(2)の半円球が合体した場合 「はじめての材料力学」サポートページ >重心の求め方について そ例題2 一様な物質でできた,底面の半径 ,高さ の円錐の重心 底面から の位置で厚さ の円板を考えると,その半径は であり,その体積は となる。 これより重心の高さ は以下のように計算できる。TZ https//sciinstrumentreponorg/?action=repository_oaipmh oaisciinstrumentreponorg TZ

ジャズドラムにおけるスティックの選び方 チップ 重心編 オススメスティック 奥村純平 Official Site
円錐 重心
円錐 重心-一様な剛体,質量M,重心を通る軸 ( p92) 2 5 2 I = Mr 2 2 1 I = Mr 2 10 3 I = Mr 半径 r の球 半径 r の円錐 半径 r の円板, 円柱 回転軸 r 回転軸 r 回転軸 r 前回の復習 工学院大学の学生のみ利用可:印刷不可:再配布不可 加藤潔 18 21※重心は \(g\) を用いることが多いです。また、他の三角形の重心については、高校生になってから学習することになります。 重心の位置がどこなのか。 それを知るためには、\(ahhm\) が必要です。 ずばり答えを書けば、 \(ahhm=21\) です。 下の図において、 水色の三角形と、赤い三角形の面積




物体の重心について 画像の問題でこの板から図のように1 4を切り取るので Okwave
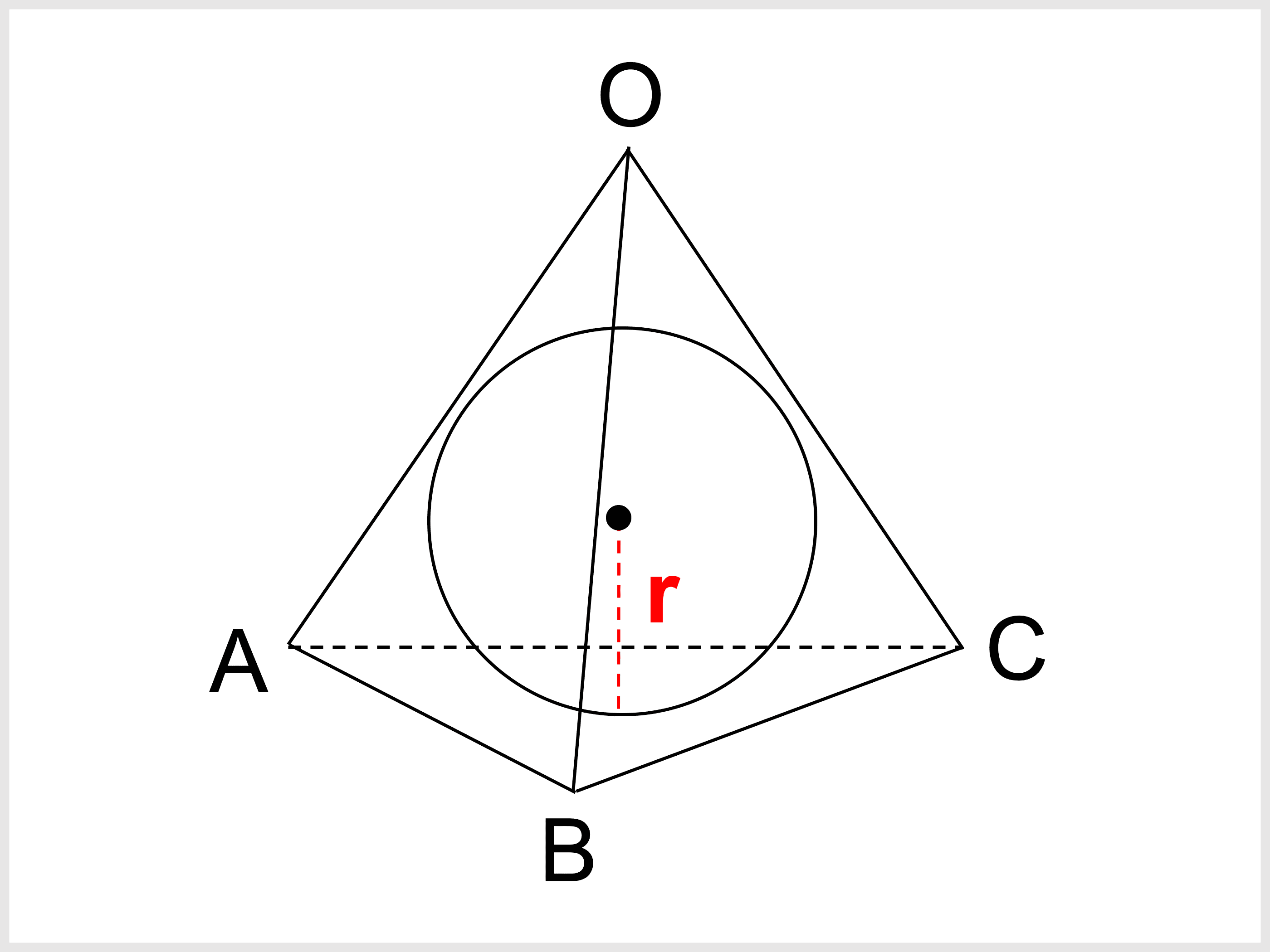
Bunryu Kamimura 三角錐の重心は3:1の所にある。 証明 三角錐の重心は、各面の重心と頂点を結んだ線上にあるはず。 それをGとする。 ALD: DLE=2:1= ADG: DGE DGE: DGK=3:2 よって ADG: DGK=6:2=3:1=AG:GK 円錐だとどうなるだろうか?直円錐 P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの強さ P102 ばねの図表 P111 ばねの一般計算式 P112 伝熱計算の式(表面温度を設計条件とする場合) P121 主要化学工学公半径r,高さhの一様な円錐 の重心の位置を求めよ r h 中心軸上にあることは明白 なので,その位置を求める この線上にある 工学院大学の学生のみ利用可:印刷不可:再配布不可 加藤潔 18 24 x x =0 x = h 断面図 2 2 4 1 = πr h 分子 ∫ h xS x dx 0 ( ) 2 2 2
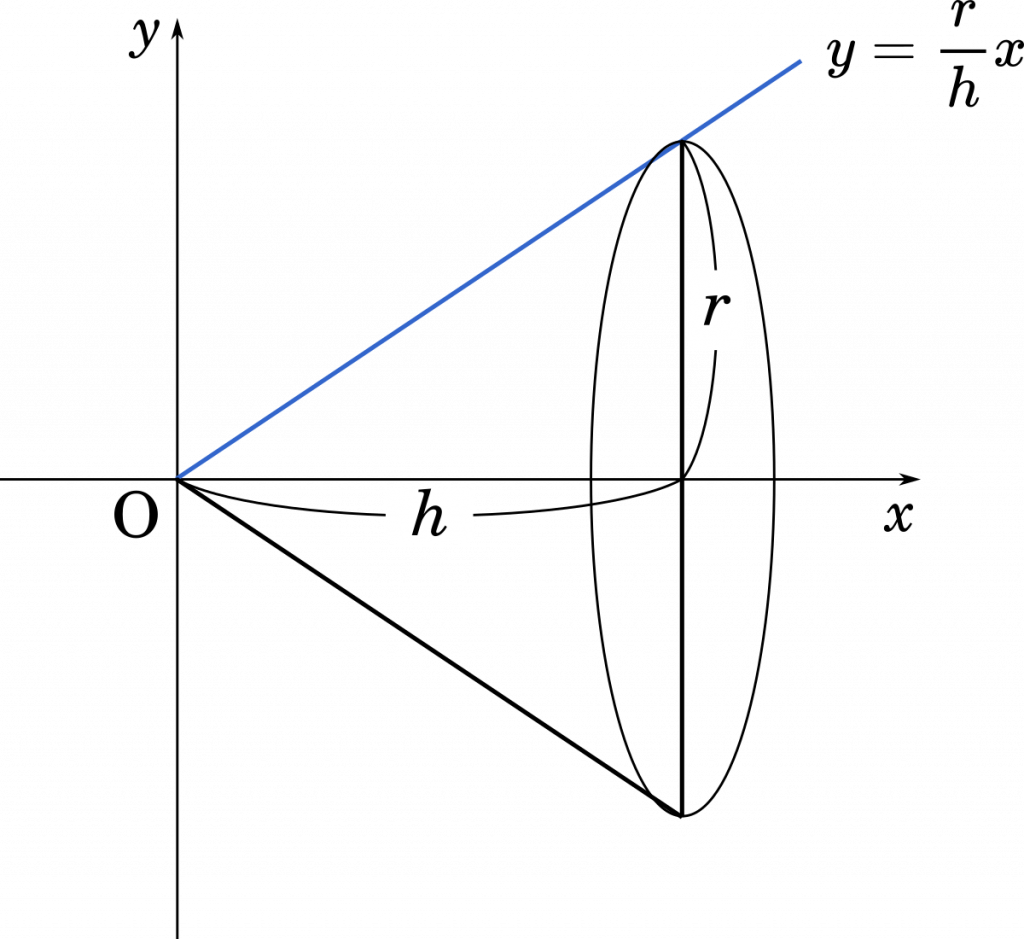
「底面のない」はわかりますが、円錐の頂面とは? 円錐の高さをLとし、底面の半径をrとした中空の円錐の側面だけのものを考え、その重心の位置を x0 とします。(2) 円錐の頂点からz だけ下で,底面と平行な方向にスライスした,厚さdz の円盤の慣性モーメ ントは dI = ˆ ∫ r e 0 (2ˇr)drr2 dz = 2ˇˆ r4 4r e 0 dz = 1 2 ˆˇr4 e dz ここでre は円盤の半径であり,z に比例して線形に増加する.すなわちre = Rz=H と表すこ とができる.この関係を代入して dI = 1 2 ˆˇ (R円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積
作成者 Bunryu Kamimura 三角錐の重心から円錐の重心へ 三角錐の重心は底面から高さ4分の1の所にあります。 円錐は無数の三角錐に分割することができます。 それらの三角錐の重心の重心はどこにあるのでしょうか? 円錐の重心の位置が側面から頂点までをhとすると 重心G(x、y)はy=1/4×hになります。 また、半球は半径r、重心(x、y)とすると y=3/8×rになります。 なぜこのような式が導かれを得る.すなわち,直円錐の重心は対称軸上にあり,頂点から全体の高さの 3/4 だけ離れたところにある. 剛体の運動は,重心の並進運動と,重心のまわりの回転運動とに分解される. 剛体全体の運動エネルギーK は K = K重心K回転 (G10) と書くことができる,ここで K重心= 1 2 M d2 dt2 R⃗(t) (G11




重積分 重積分について 問題を解いてください 形状d物体の密度がr Okwave



1
V=容積、S=表面積、As=側面積、Ab=底面積、χ=底面より重心までの距離 截頭円垂 角 垂 球 欠 球 V=容積、S=表面積、As=側面積、Ab=底面積、χ=底面より重心までの距離 円柱・中空円柱 截頭円柱 截頭角垂 方光体 V=容積、S=表面積、As=側面積、Ab=底面積、χ=底面より重心までの円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることによりAuthor Masaki Created Date PM



Ppt 熱流体力学講義 番外編 Powerpoint Presentation Free Download Id



Freecadの加算パイプの変わった使い方 円錐 正四面体の作成方法 3pysci
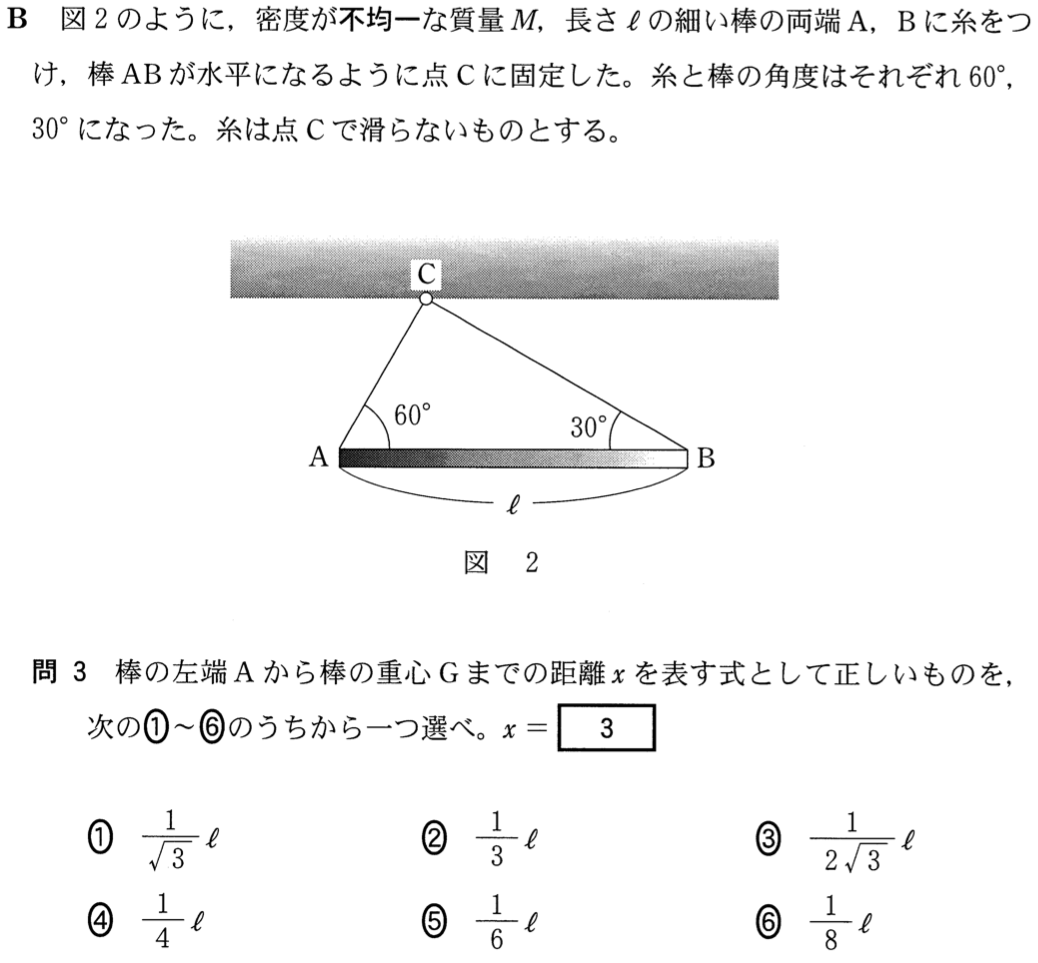
まず始めに、重心を通るある軸の周りの回転運動について考えてみる。固定軸の方向を z 軸と する。剛体中に含まれる質点の座標と質量を(xi,yi,zi)、mi としたとき、角運動量のz 成分は以 下のように表される。 Lz = ∑ i m ir 2 dθ dt = I dθ dt, I ≡ ∑ i mir 2 i (51) ただし、極座標を用いてxi = ri cosθi, yi 重心が 軸上にあることは対称性から明らかなので, 軸方向の重心位置だけを式(7)(8)を使って求めることにします.質量 が次のようになるのは良いでしょうか.円錐の体積の公式を使いま円錐 縦×横×高さ (半径)2×314×高さ 台形を2つの三角形に分け、その重心を結ぶ直線とAD、 BCの中点を結ぶ直線MNの交点 半円筒形は、物体の外側に重心が位置する。半円筒形を 小さく分割し、分割したそれぞれの重心の合力により 重心位置を求めると、右の図のような位置になる。 2つの面の
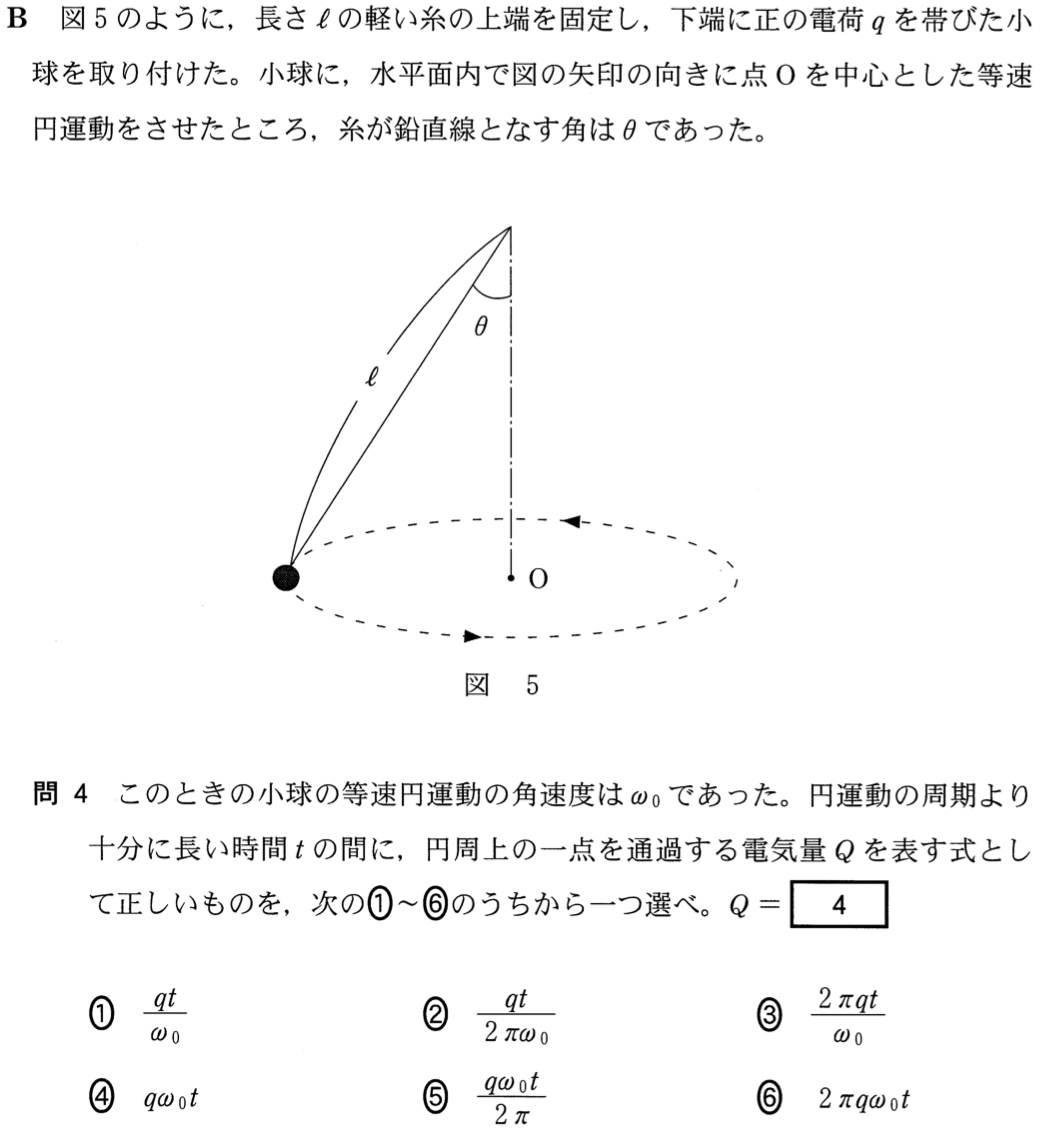



センター15物理追試第2問b 円錐振り子と磁場 理科が好き Com




M Sudo S Room 円錐台の慣性モーメントの導出法
円錐台の側面積,体積,重心の公式など. 4.任意多角形のモーメント計算公式集 PDF および Excel ファイル販売 自分で考案した任意多角形の面積,重心 (図心),断面モーメント,慣性モーメントの公式集 PDF ファイルおよび Excel ファイルを,DLmarket 様にて委託ダウンロード販売しています高さ の直円錐の重心の位置は であることが分かる。 この円錐の質量を とする。 同様に、切り取られた上部の円錐部分の重心位置は 、質量は と求められる。 切り取った後の円錐台の重心の位置を とすると、 したがって、底面からの高さは、 物理学ii 第2 回 中間テスト 2. 輸送機が滑走路に重心を求める公式がある。これは、図形の面積をSとしたとき、 重心の座標(x G ,y G )は、x G G である。 ここでdsは、それぞれの積分方向における面積の微小増加量である。 ①正三角形の重心 簡単な例として、この公式を使って、右図のような 一辺の長
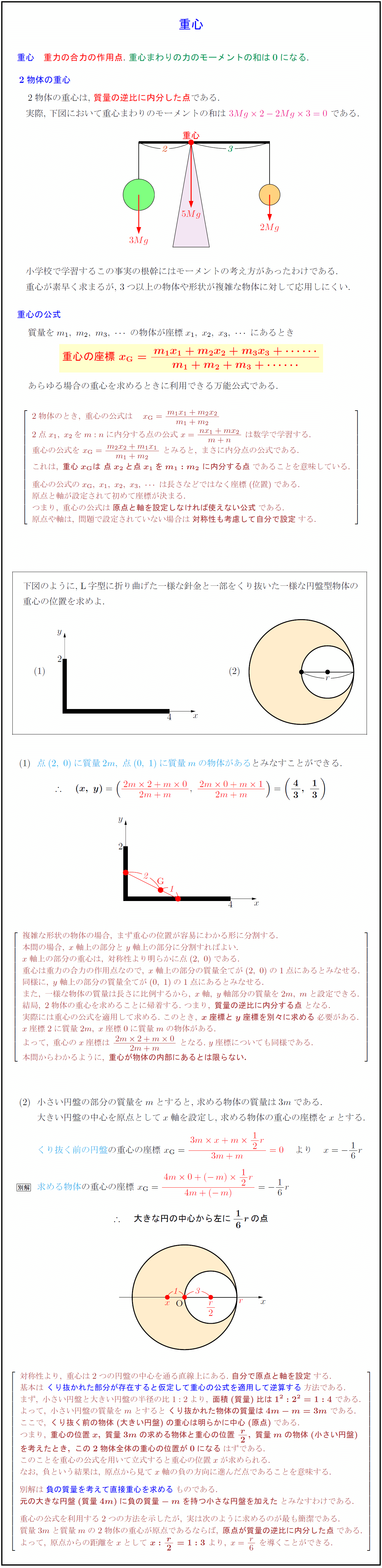



高校物理 剛体の力学 重心 L字型物体 一部がくり抜かれた物体 重心の公式 受験の月




14 号 手回し式独楽 Astamuse
円錐 慣性モーメント 頂点が原点にあり、y軸に重心軸がある円錐に関して、x軸周りの慣性モーメントの求め方を教えてください 拙い文章で申し訳ありません 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。 これなら3秒で円錐の体積を計算できこの円錐曲線は,重心座標ではどのような方程式で表されるのか. これを明示的に表すために, , , とする. 重心座標が の点は直交ユークリッド座標では



画像をダウンロード 球 展開 図 書き方




体積 27 円錐の回転体 怜悧玲瓏 高校数学を天空から俯瞰する
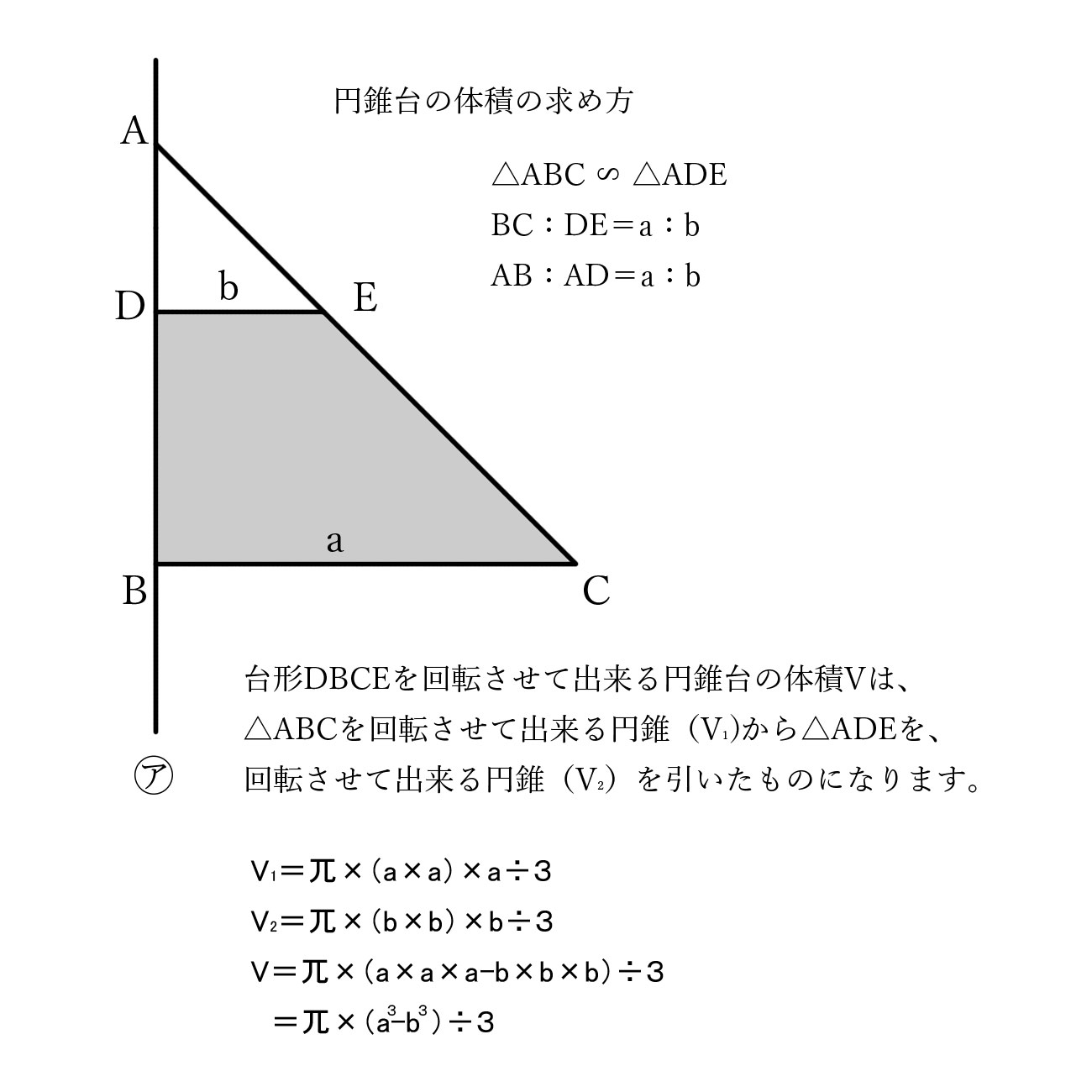
慣性モーメントの導出:円錐 21年1月12日 以下のような円錐の慣性モーメントを求めます 密度はρ、質量はmとします まずはz軸まわりの慣性モーメントを求めます 以下の図のように円錐をz軸に垂直な面でスライスします スライスした円板部分の質量は ここで、三角錐の底面の三角形BCDの重心Gを定めると、 Gの座標は、 G((bcd)/3,(efg)/3,(hkm)/3)=-A/3 になり、 OGは0Aに平行で長さが3分の1 の関係があることがわかります。 すなわち、AGは重心O点を通ることがわかり、 読者になる schoolmath's diary 三角錐の重心(四円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S



センター15物理追試第4問b 重心 力のつり合い 理科が好き Com



三角形の重心 重さあり Geogebra
切り抜かれた円盤の重心 下図に示すように, 密度が一様で半径 r の円盤1から, それに内接する半径 r 2 の円盤2を切り抜いた物体について, 次の問に答えよ この物体の重心を求めよ この物体の重心を求めよ N 個の質点の位置 (または物体の重心)と質量が



Http Www Jpho Jp 15 Prechall15 Prechall 1502 Solution Pdf




円錐台 Wikipedia



最高のコレクション 円錐 台 表面積 やもが




重心 Y社長の釣士道日記part2
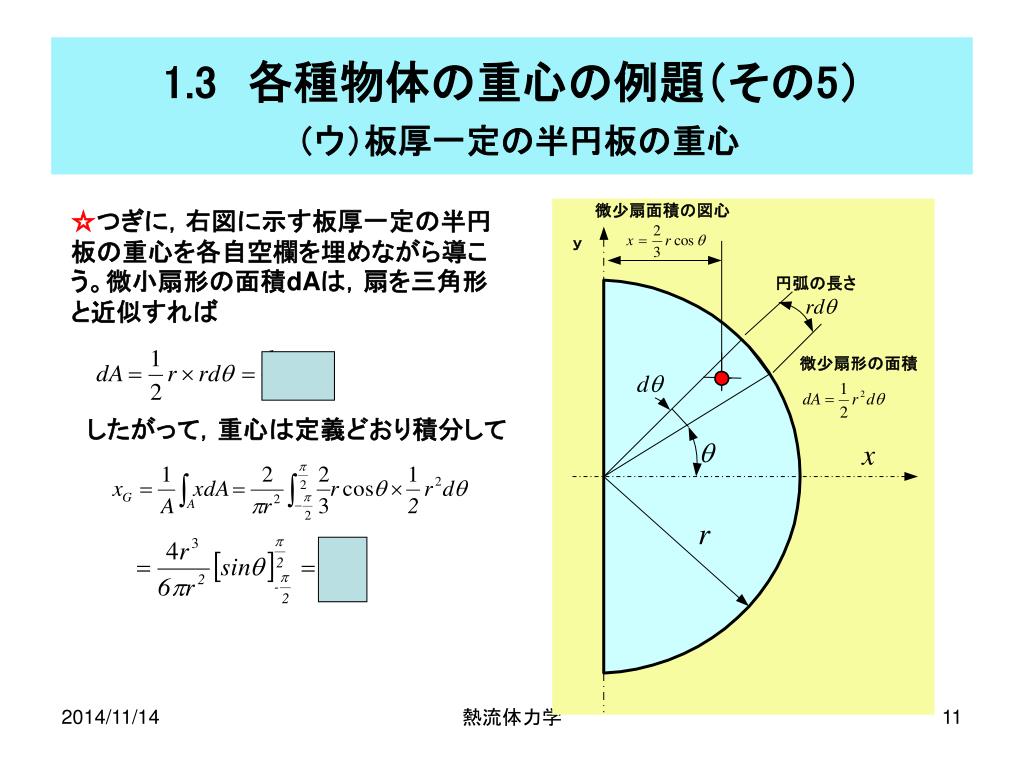



Ppt 熱流体力学講義 番外編 Powerpoint Presentation Free Download Id




回答お願いします Clear




ジャズドラムにおけるスティックの選び方 チップ 重心編 オススメスティック 奥村純平 Official Site




重心を計算して求める 5 Youtube



1
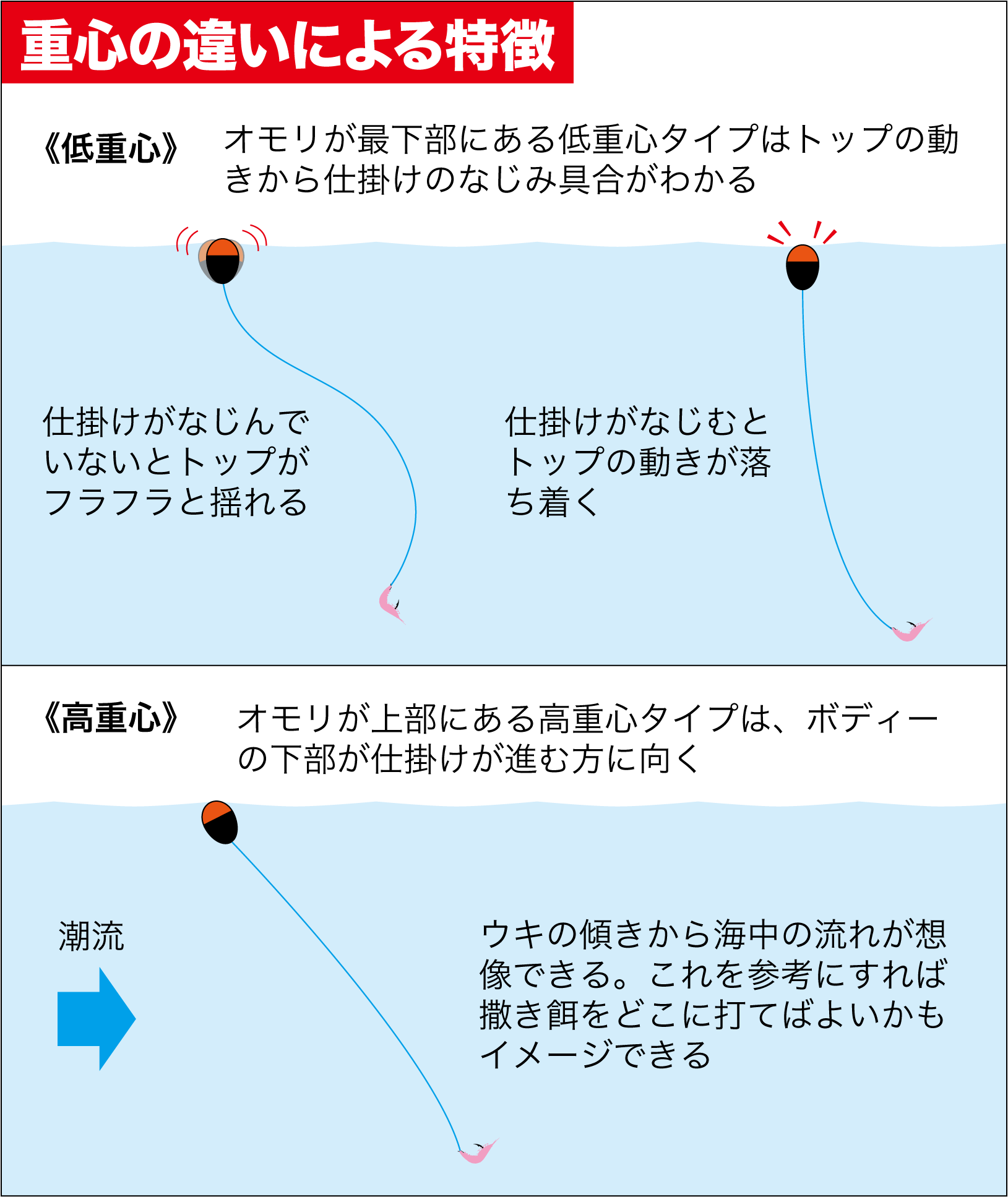



チヌ フカセ釣りの悩みを解消 高重心と低重心の円すいウキの使いわけ方法は 関西のつりweb 釣りの総合情報メディアmeme
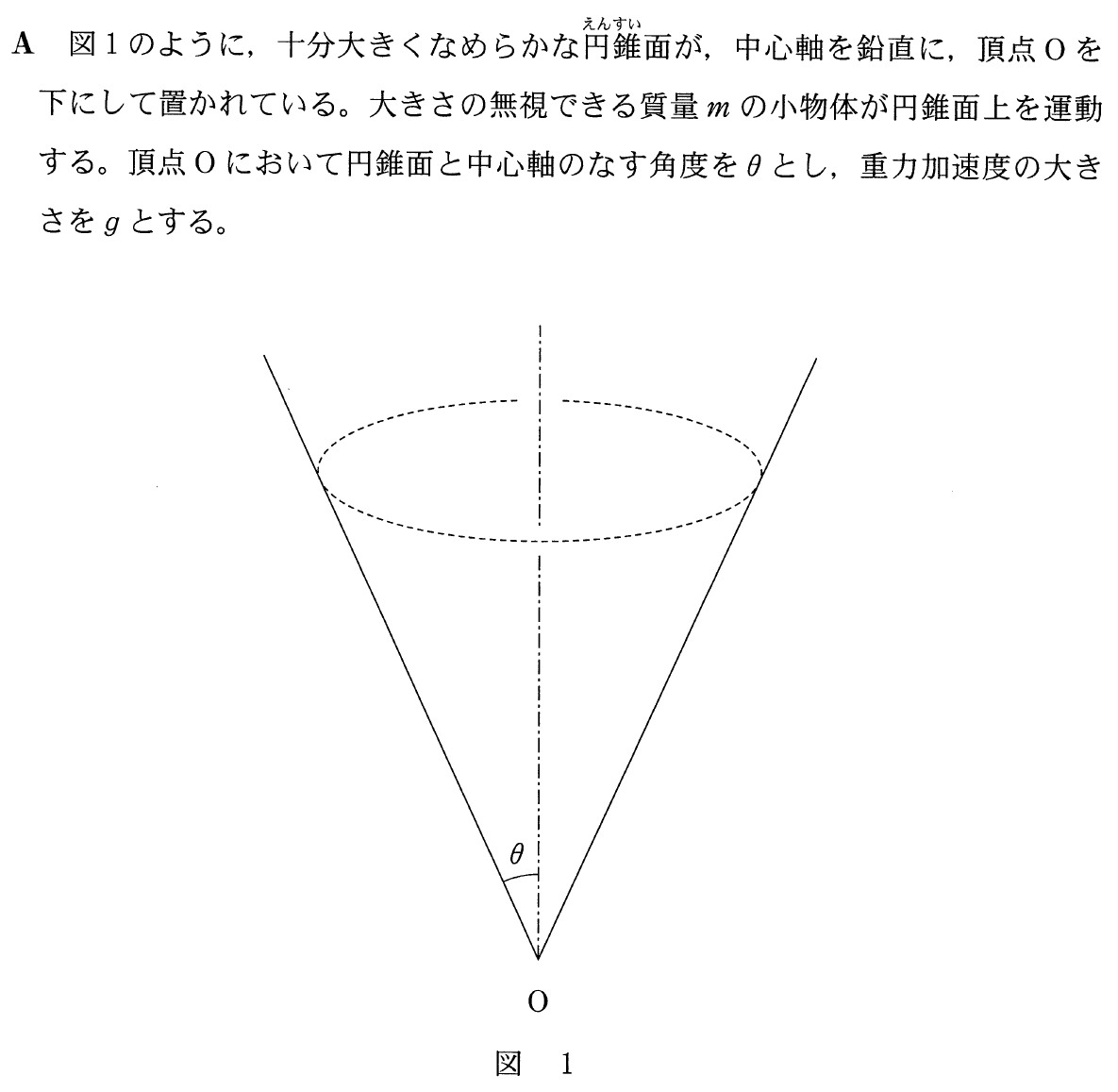



センター17物理第4問a 円錐面内での運動 理科が好き Com




基本 円運動演習1 円錐振り子 Physicmath フィジクマス
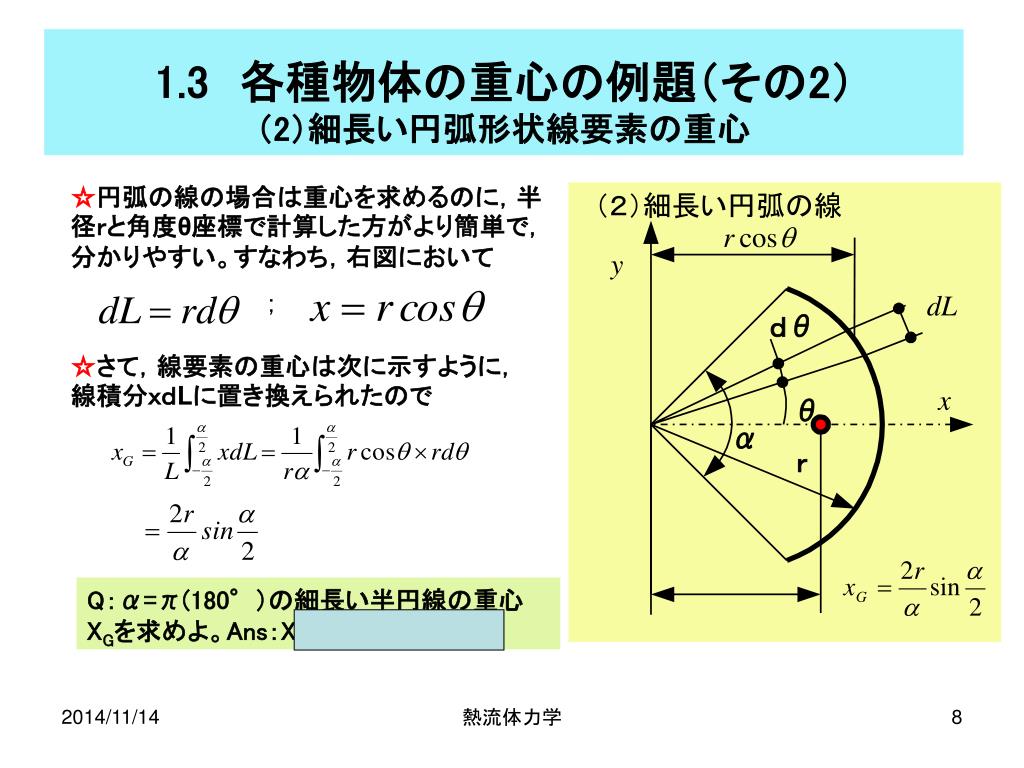



Ppt 熱流体力学講義 番外編 Powerpoint Presentation Free Download Id




体積 27 円錐の回転体 怜悧玲瓏 高校数学を天空から俯瞰する
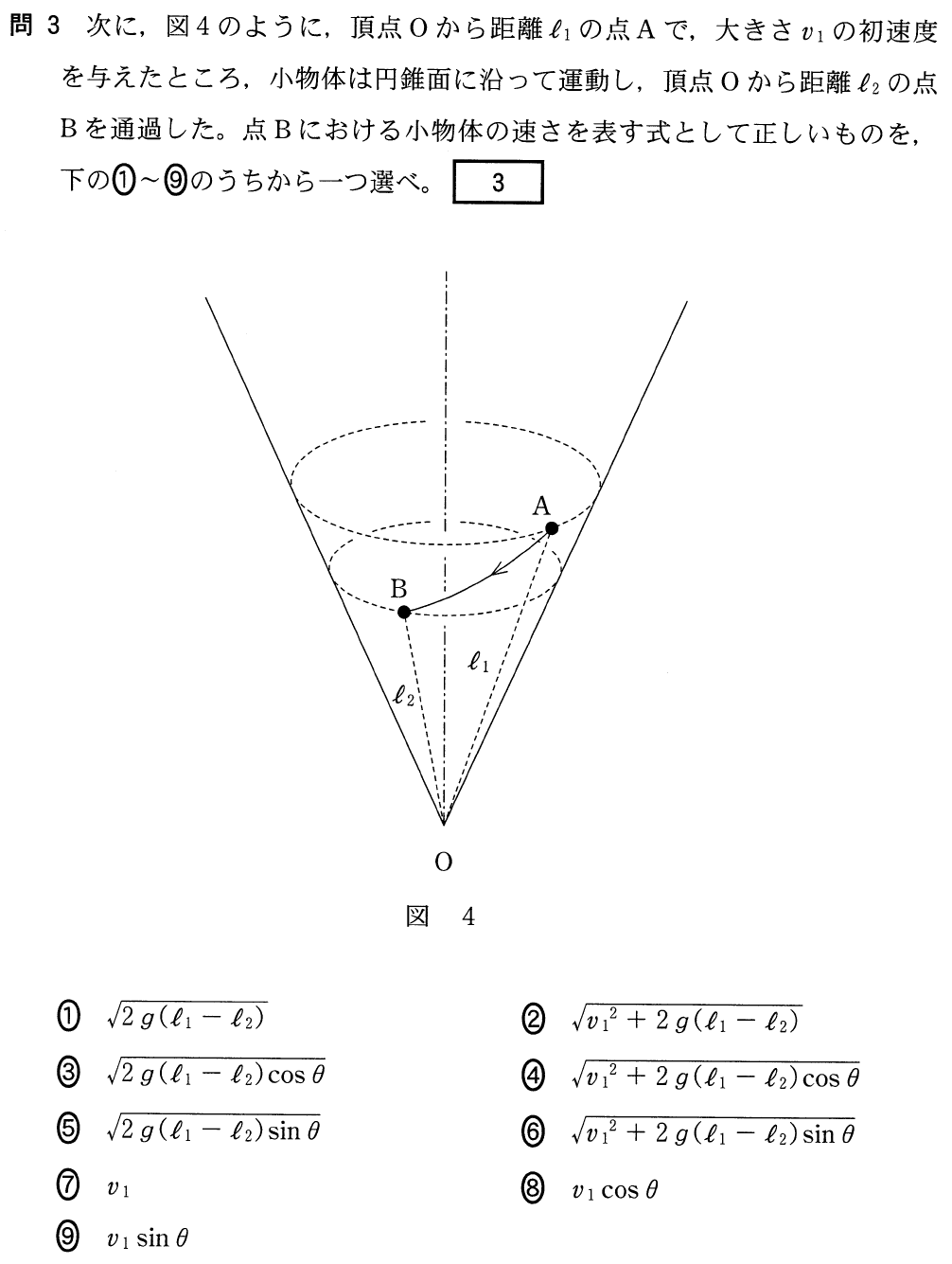



センター17物理第4問a 円錐面内での運動 理科が好き Com
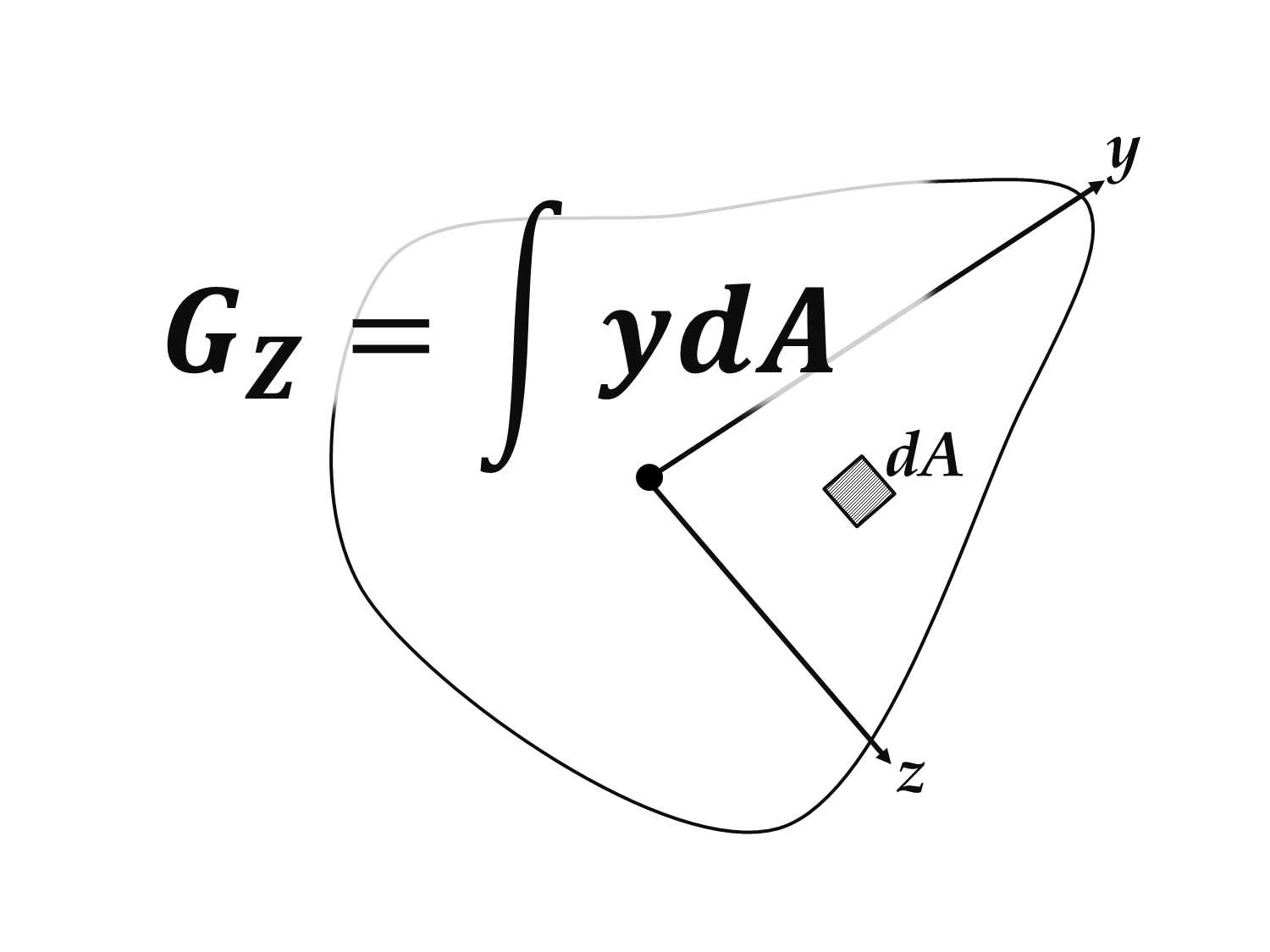



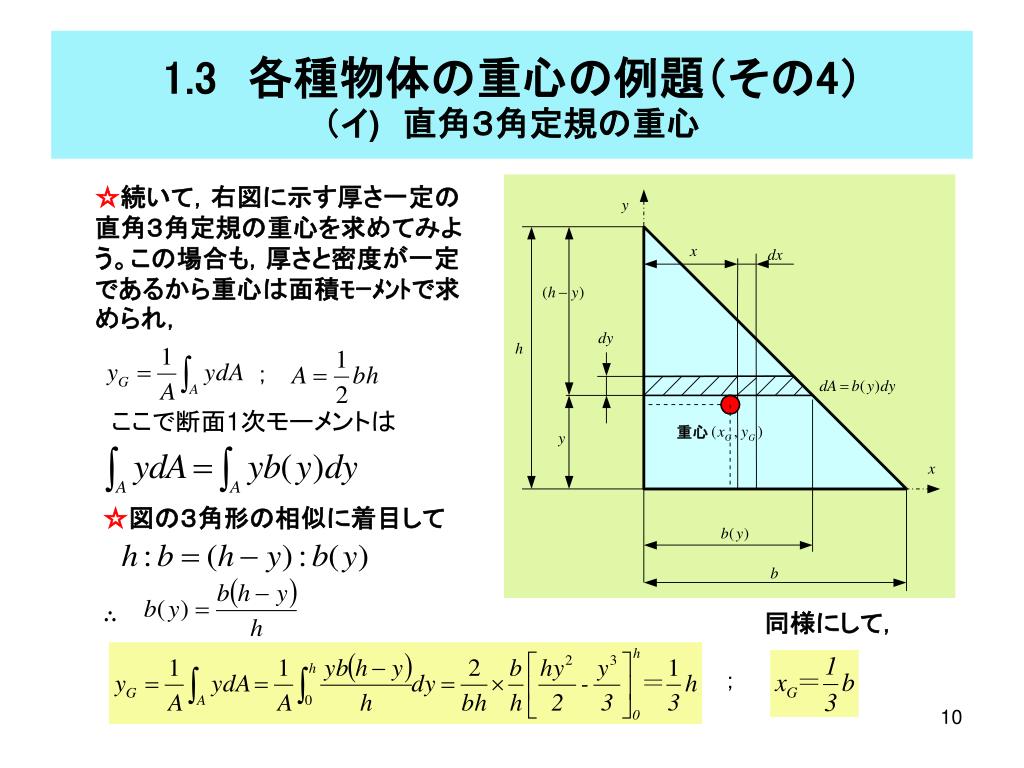
断面1次モーメントとはどんな量 その意味やイメージを解説




中古 Huf Circle H Stash Ring 輪っか 21号 Gld 服飾雑貨どこかよそに Doorswindowsstairs Co Uk




Amazon Neoformers 知育玩具 おもちゃ 積み木 ブロック 磁石ブロック 立体 パズル 誕生日 入園 入学 お祝い クリスマス プレゼント 出産祝い 女の子 男の子 子供 1歳 2歳 3歳 モンテッソーリ教育 受験 図形 展開図 学習 教育玩具 ネオフォーマー 刻印あり 5ピース




チヌ フカセ釣りの悩みを解消 高重心と低重心の円すいウキの使いわけ方法は 関西のつりweb 釣りの総合情報メディアmeme




高感度 低重心 ウキ 商品追加値下げ在庫復活 堤防 磯 夜釣り 円錐 昼夜兼用 Br425 中通し 電気ウキ




円錐の体積を求める Youtube



Misc Mathematics Lecture
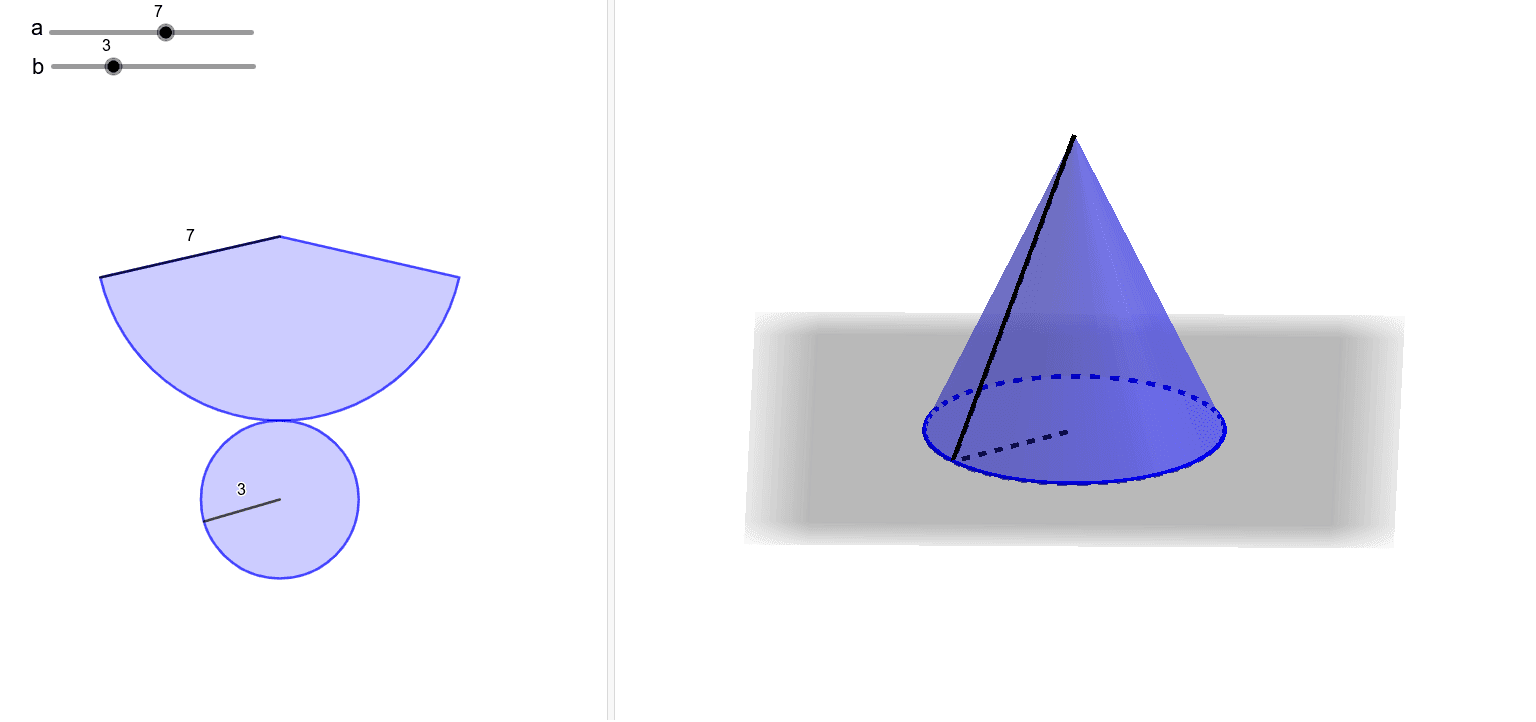



円錐の展開図 Geogebra



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



Q Tbn And9gcqjobggcmt23 2z3kno11yv3jyxklvrxkobpwlhwovwikso5zii Usqp Cau



頭の体操 問題3 解答 Cometのサボテン栽培日記



Misc Mathematics Lecture




小林晋平 振り子の波 Pendulum Wave です 妻のアイデアで手芸用ビーズを使いました ボール状のおもりより重心の位置が分かり易く調整も楽です 不器用な僕をみかねて調整は妻がやってくれたのですが 二本の紐で支える形になるので 絡んだり円錐




M Sudo S Room 円錐の側面体 円錐台の側面体の慣性モーメント



数iii積分 円すいの体積の公式を回転体の体積として求めてみる 公式に1 3がある理由 Mm参考書




Amazon スーパーロボット超合金 漢のドリルセット フィギュア ドール 通販



テトラポッドを作ってみよう その2 3dモデリング テトラポッド 3d楽



この円錐台の重心の位置を剛体の体積分を用いて求めたいです ただし 底面の中心を Yahoo 知恵袋




物体の重心について 画像の問題でこの板から図のように1 4を切り取るので Okwave




14 号 ジェット干渉アクチュエータおよびこれを備えた大気圏再突入機 Astamuse



Http Blog Livedoor Jp Cat Catalyst E5 86 86 E9 8c 90 Pdf
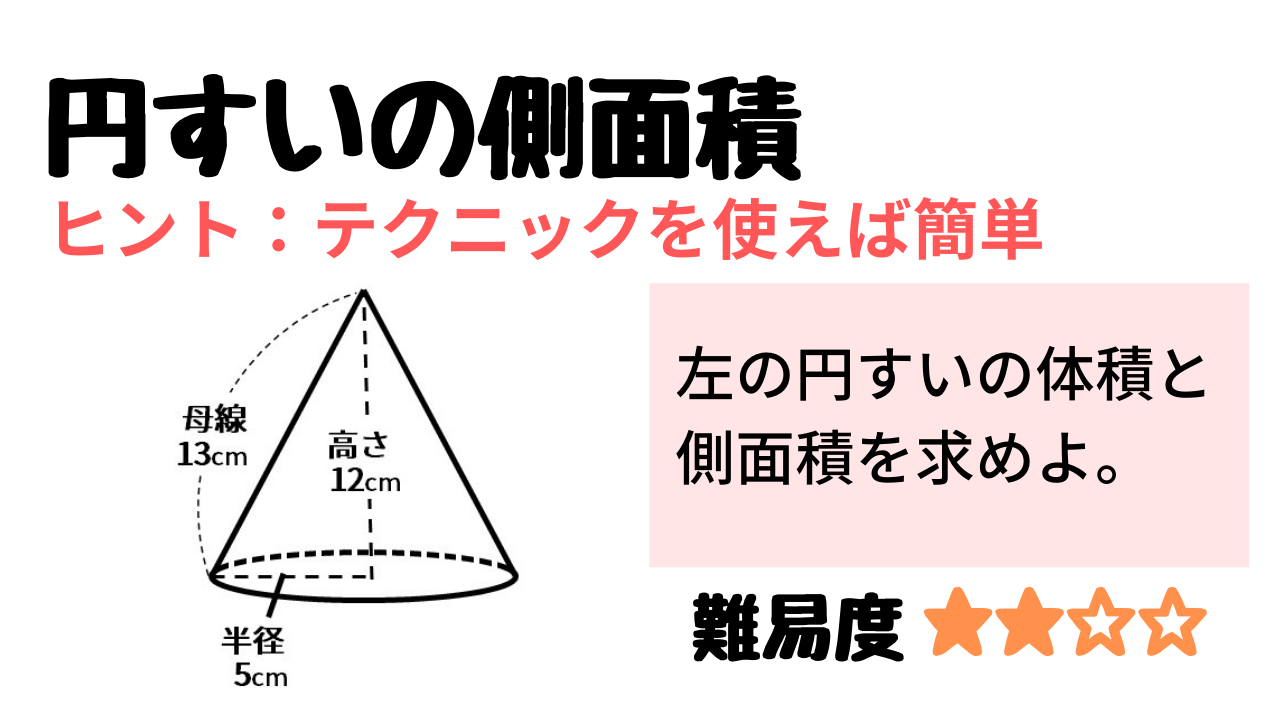



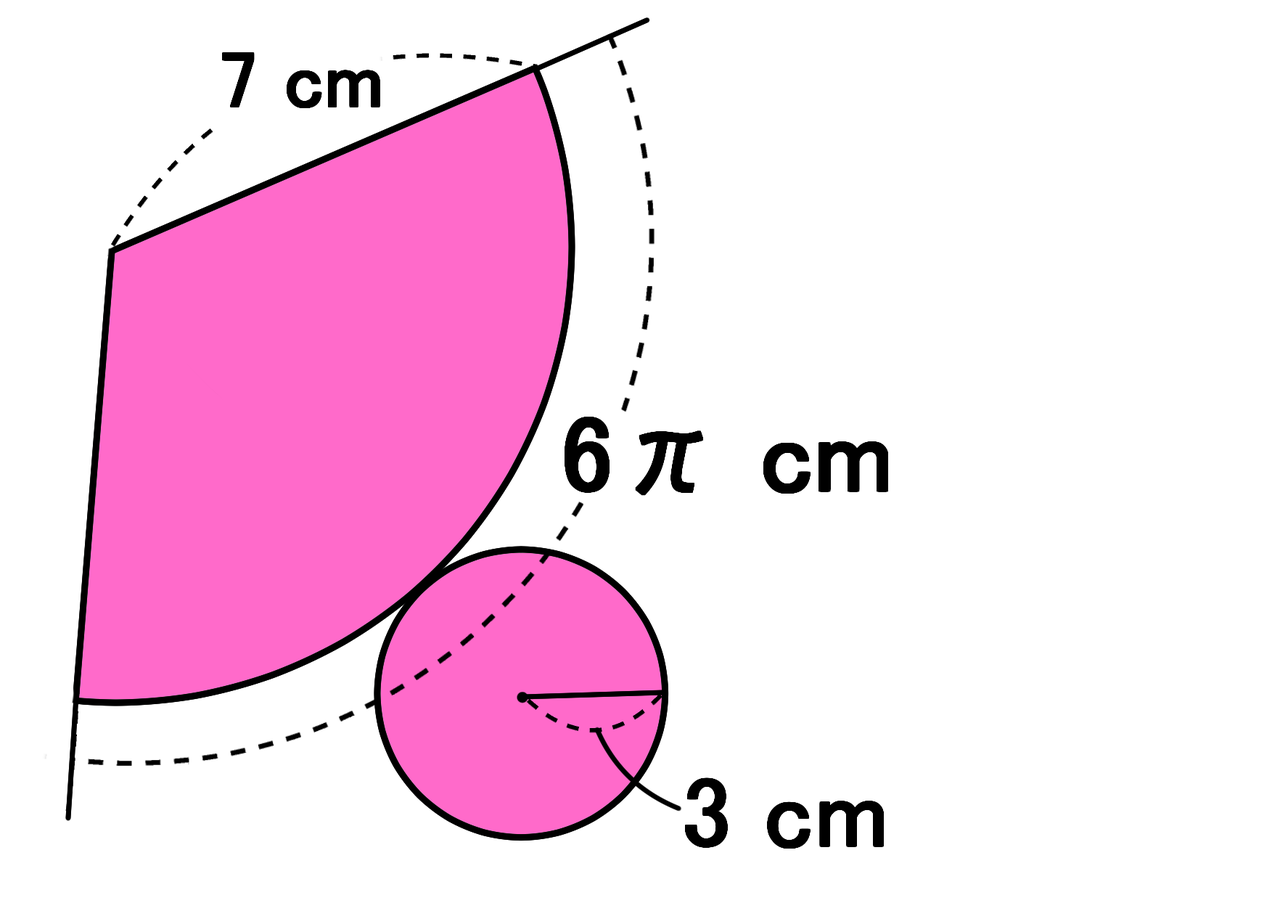
中学受験算数 円すいの側面積の問題 テクニック伝授 Stupedia
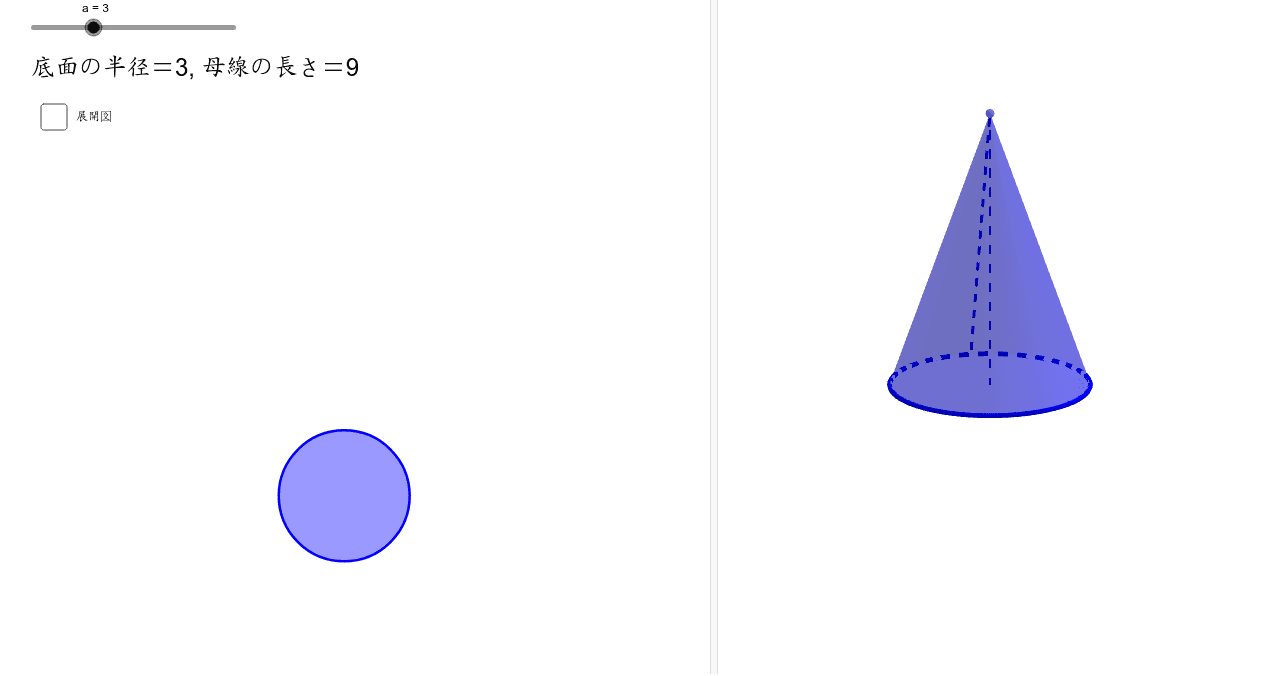



円錐の展開図 Geogebra



画像をダウンロード 球 展開 図 書き方




M Sudo S Room 回転体の重心の計算手法



Www Kri Sfc Keio Ac Jp Report Gakujutsu 08 3 8 Sb 04 Pdf
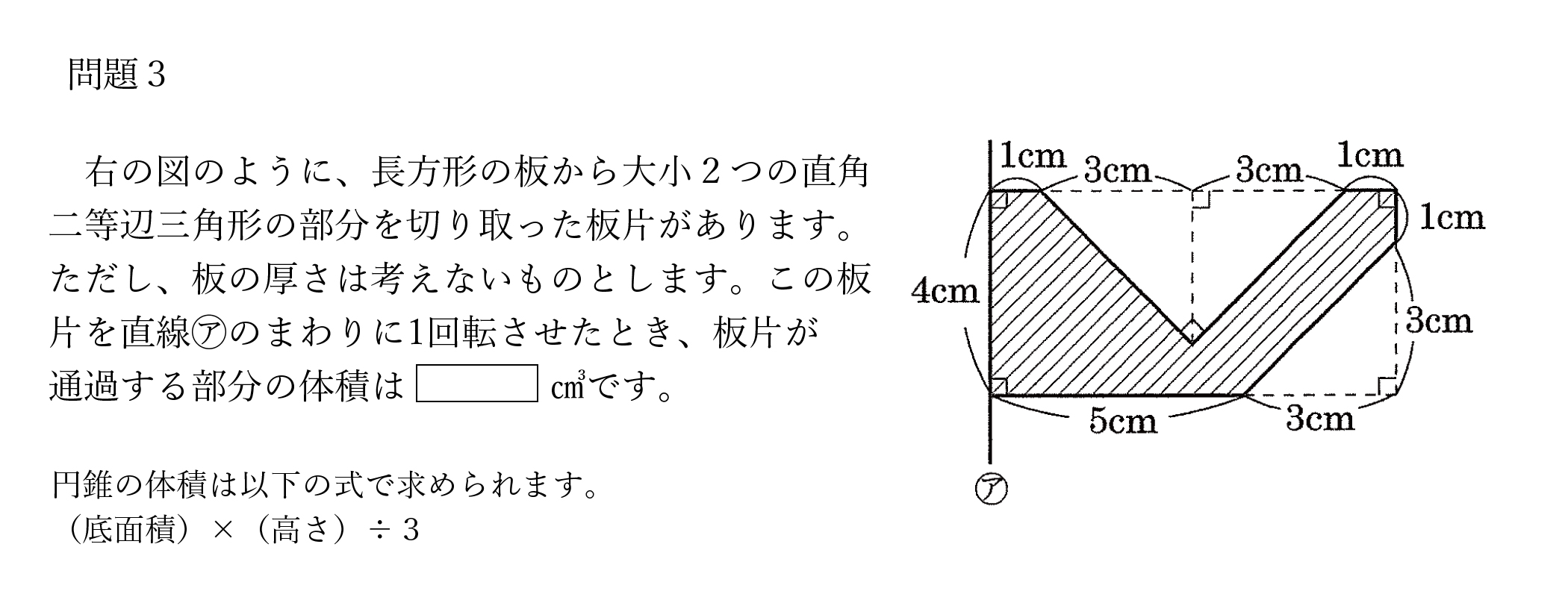



頭の体操 問題3 解答 Cometのサボテン栽培日記



Misc Mathematics Lecture




空間図形14 円すい台の体積 Youtube




14 1010号 眼屈折力測定装置および眼屈折力測定装置の校正方法 Astamuse




11 号 運動補助具 Astamuse




高感度 低重心 ウキ 商品追加値下げ在庫復活 堤防 磯 夜釣り 円錐 昼夜兼用 Br425 中通し 電気ウキ



Www Jpo Go Jp News Benrishi Shiken Mondai Document ronbun Sentaku T2 21 Pdf
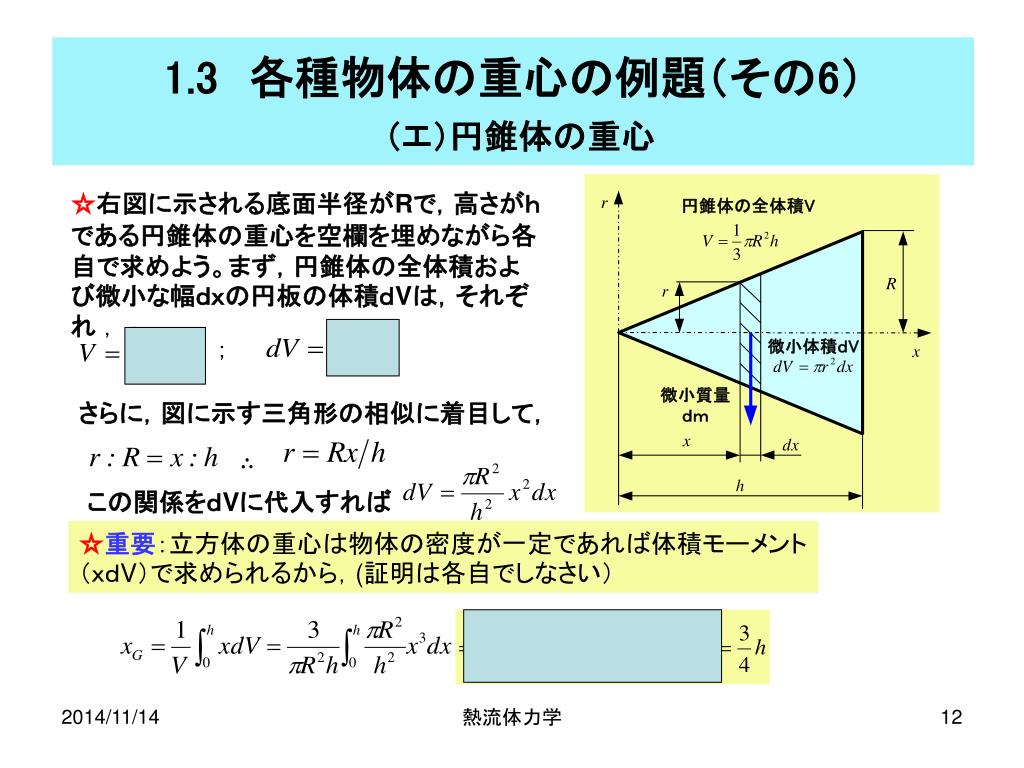



Ppt 熱流体力学講義 番外編 Powerpoint Presentation Free Download Id



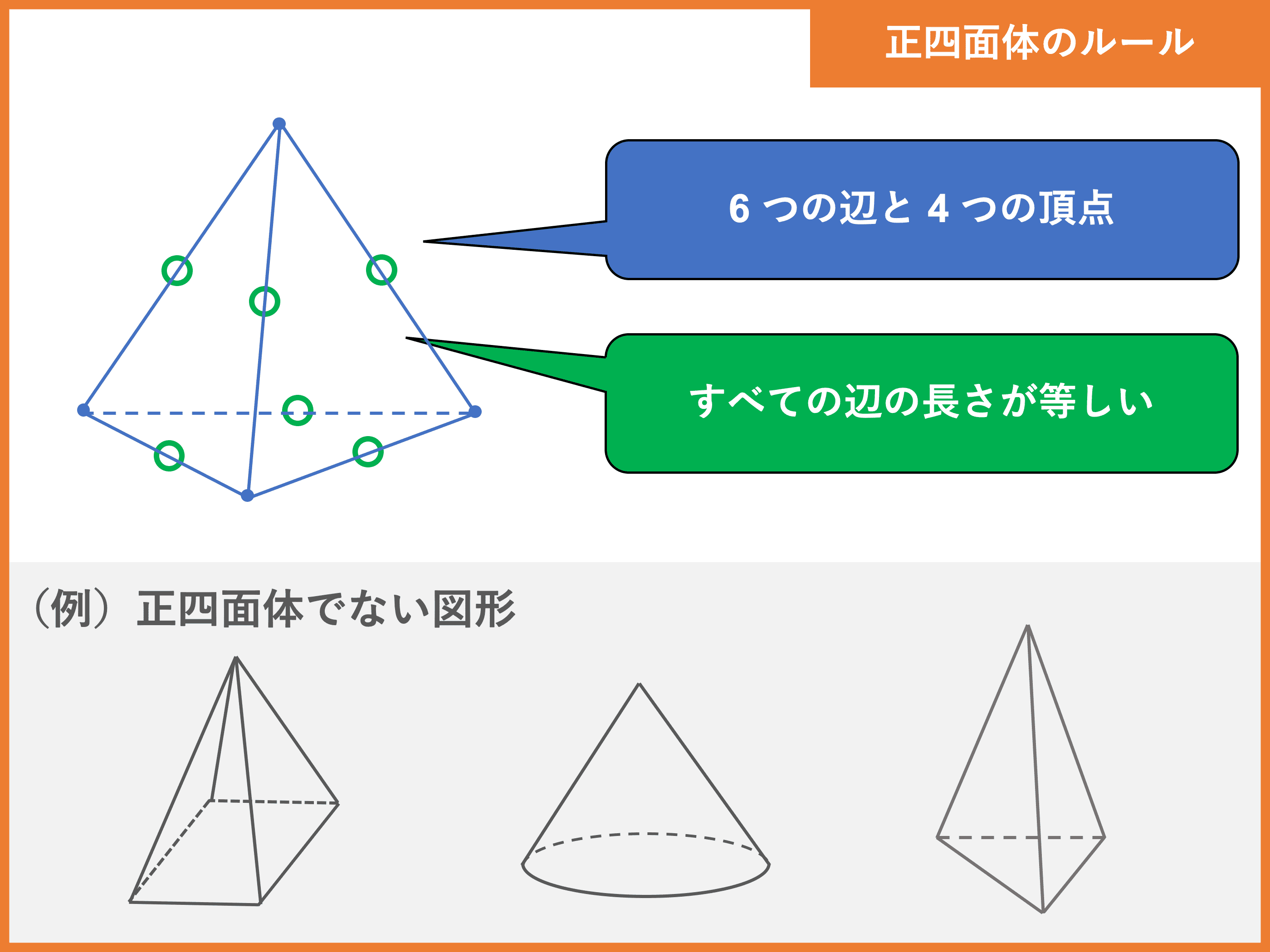
正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典
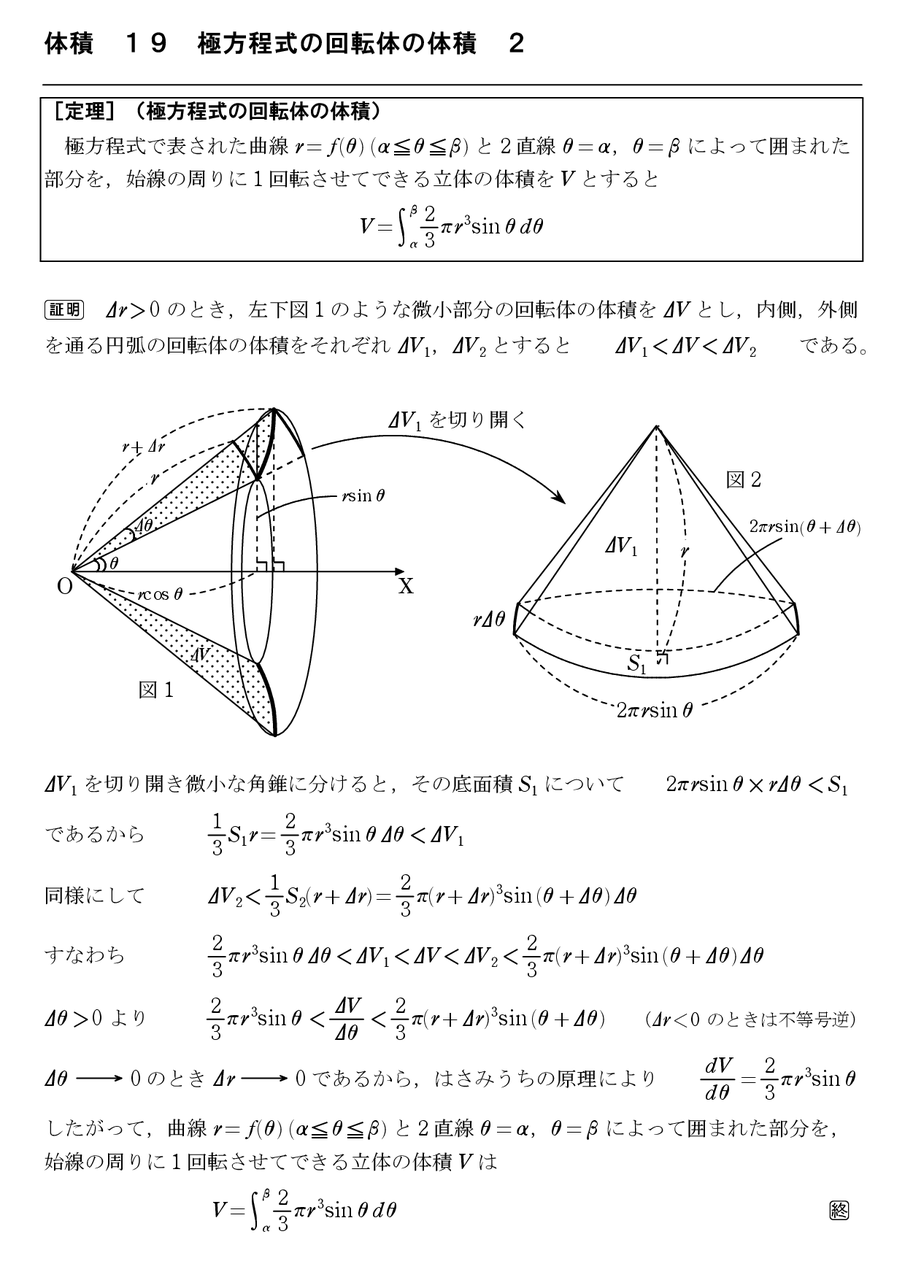



体積 27 円錐の回転体 怜悧玲瓏 高校数学を天空から俯瞰する



バロウマン方程式によるcp 圧力中心 の求め方 ブリコラージュ工房 シュレディンガーの猫
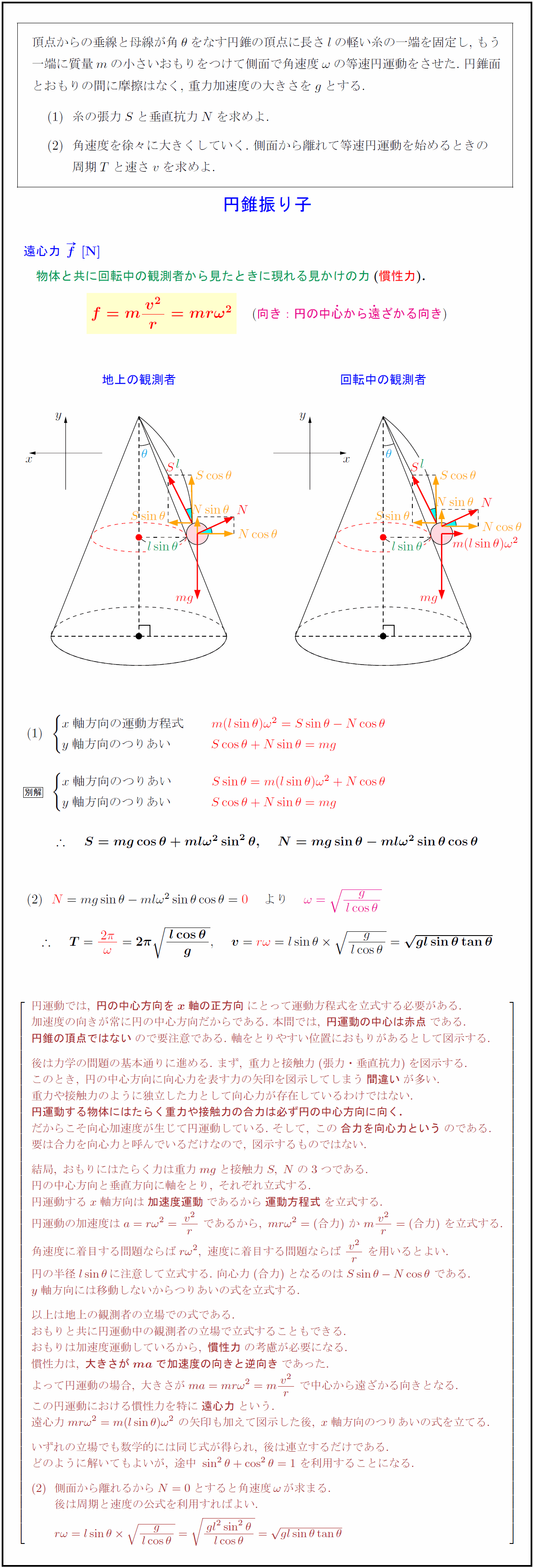



高校物理 円錐振り子と遠心力 水平面内の円運動 受験の月



10本セット スマートコーン 赤 Smt 10 資材 印刷のルネ 通販 Yahoo ショッピング



2
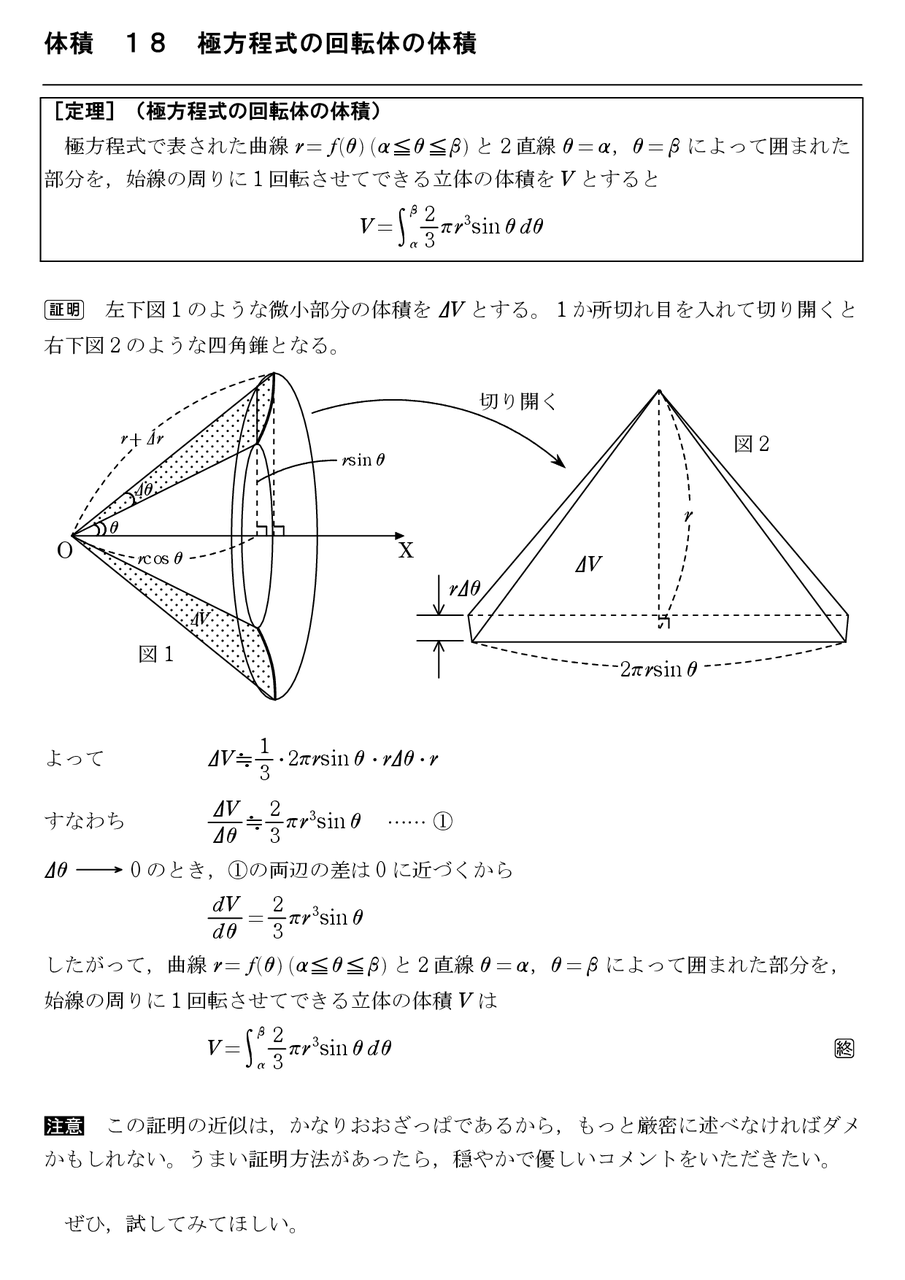



体積 27 円錐の回転体 怜悧玲瓏 高校数学を天空から俯瞰する




画像をダウンロード 球 展開 図 書き方
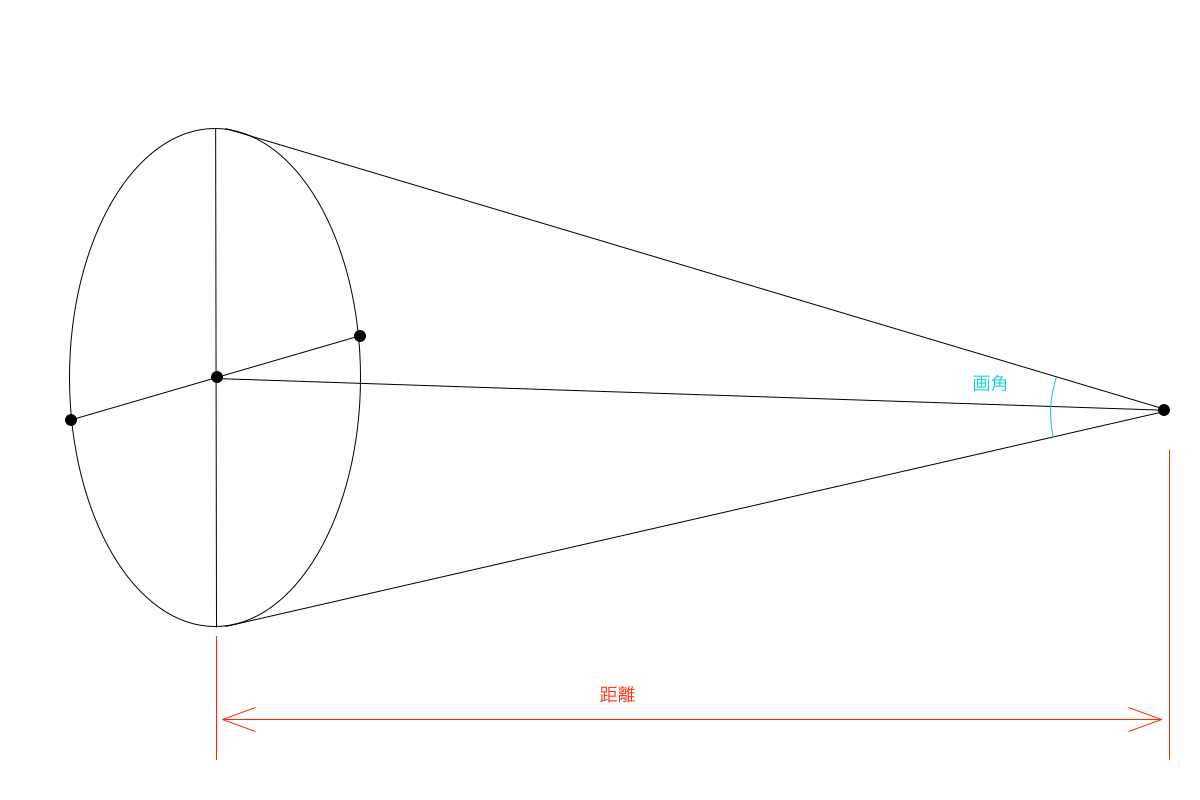



視円錐を使って考える望遠パース 広角パースの描き方



Shizuoka Repo Nii Ac Jp Action Repository Action Common Download Item Id Item No 1 Attribute Id 31 File No 1
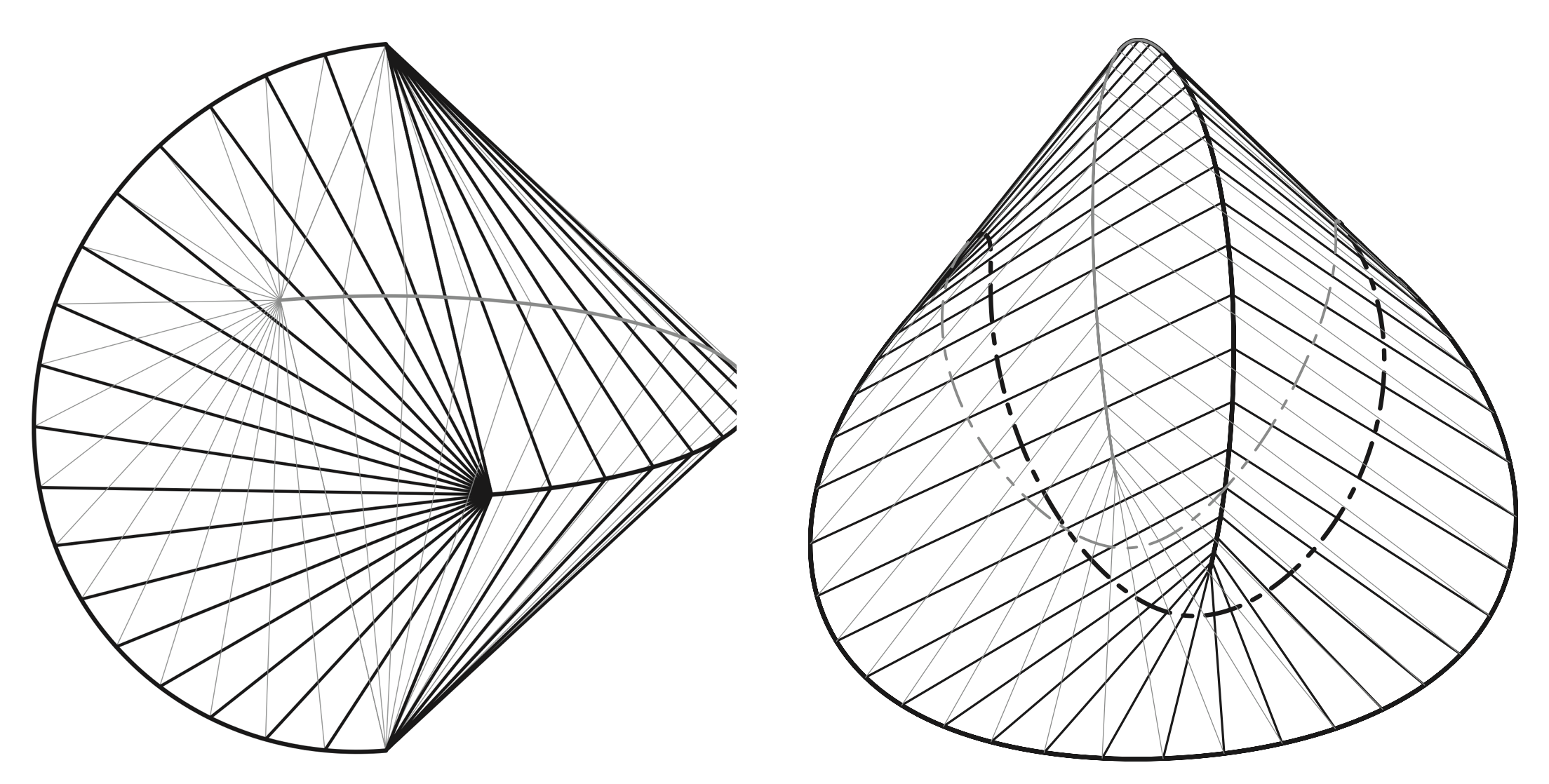



錐体の体積公式と等高重心立体に関する考察 平田浩一 ぼのぼ の ブログ




過去の展覧会 展覧会情報 大阪市立東洋陶磁美術館



2



Uedakasetsucircle3 Jimdo Com App Download E9 87 8d E5 Bf 81 Ab 81 81 84 81 A6 81 Ae E5 95 8f E9 A1 8c Pdf T




11 号 飛行体 Astamuse



二体問題 Two Body Problem




Shiratama Dango Tutorial Yande Re




はやぶさ 最近初めて知ったんですけどね 銃弾の重心と空気抵抗から受ける力の重心 がほんの少しズレているから 放物線を描いて飛翔する弾丸は最終的に円錐を描いて回転するらしいんですよ奥さん
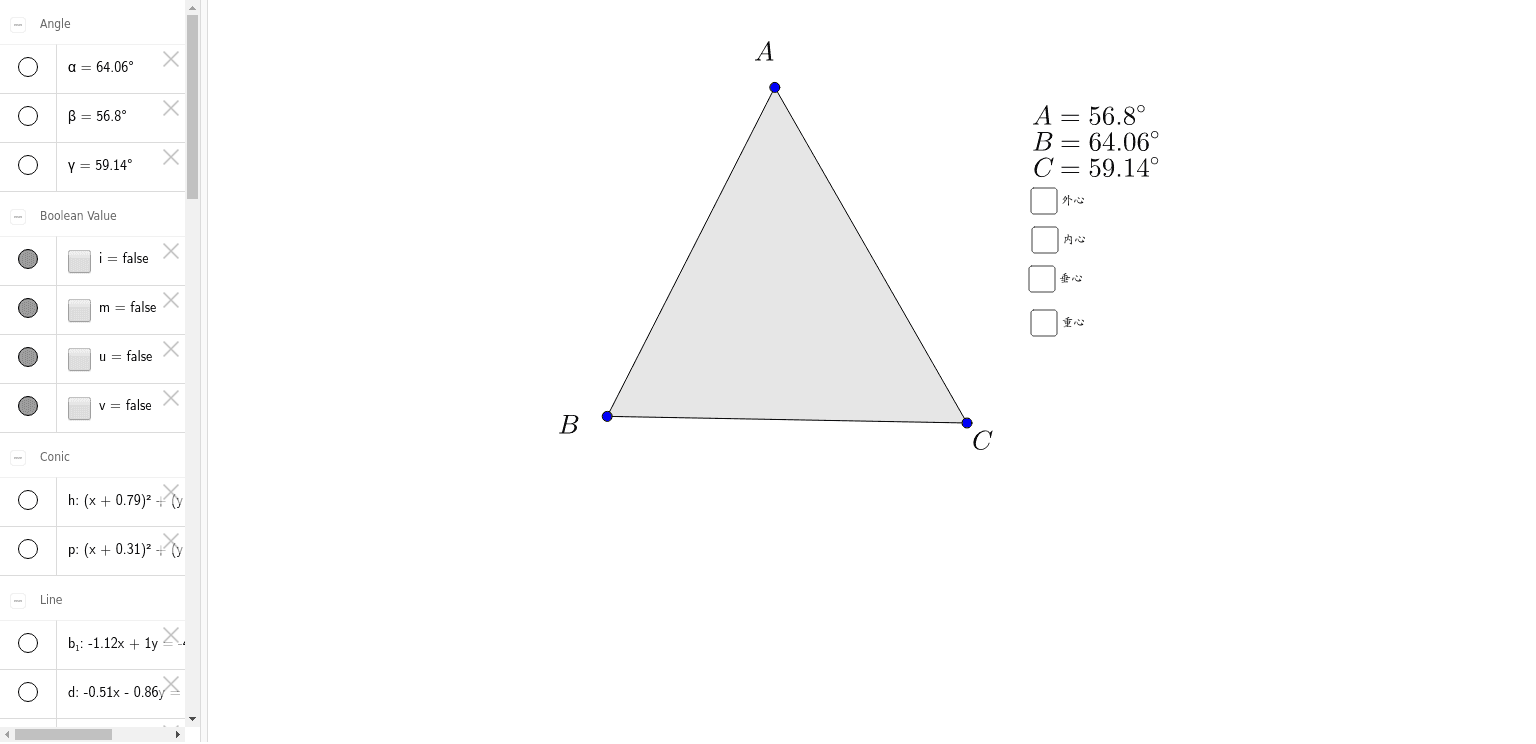



三角形の外心内心垂心重心 Geogebra




重心を低く Soraiz
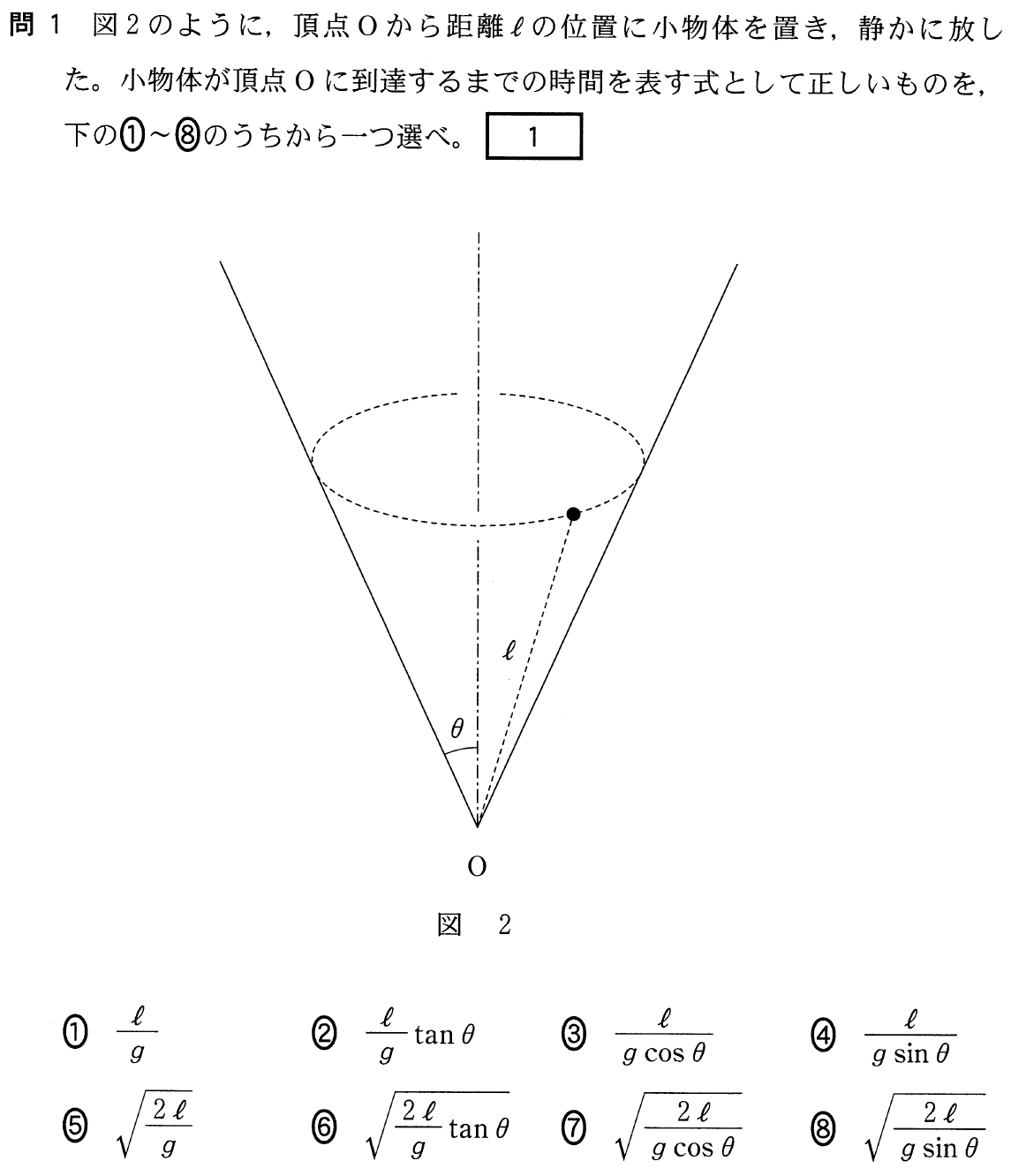



センター17物理第4問a 円錐面内での運動 理科が好き Com



1
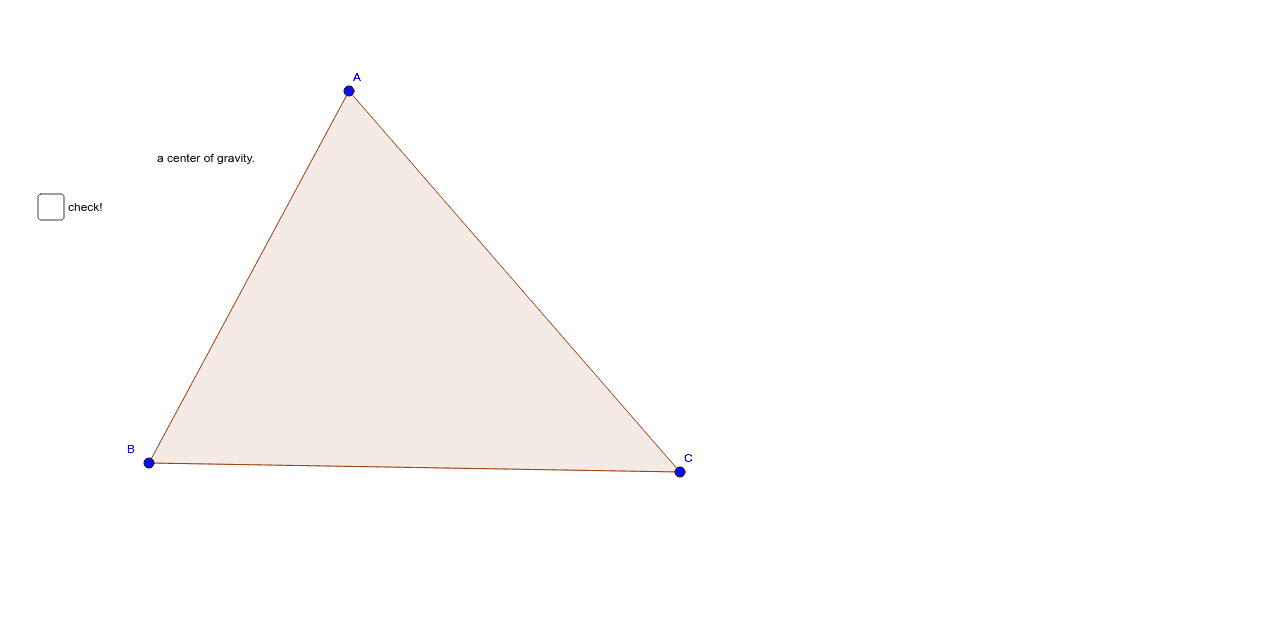



三角形の重心 A Center Of Gravity Geogebra
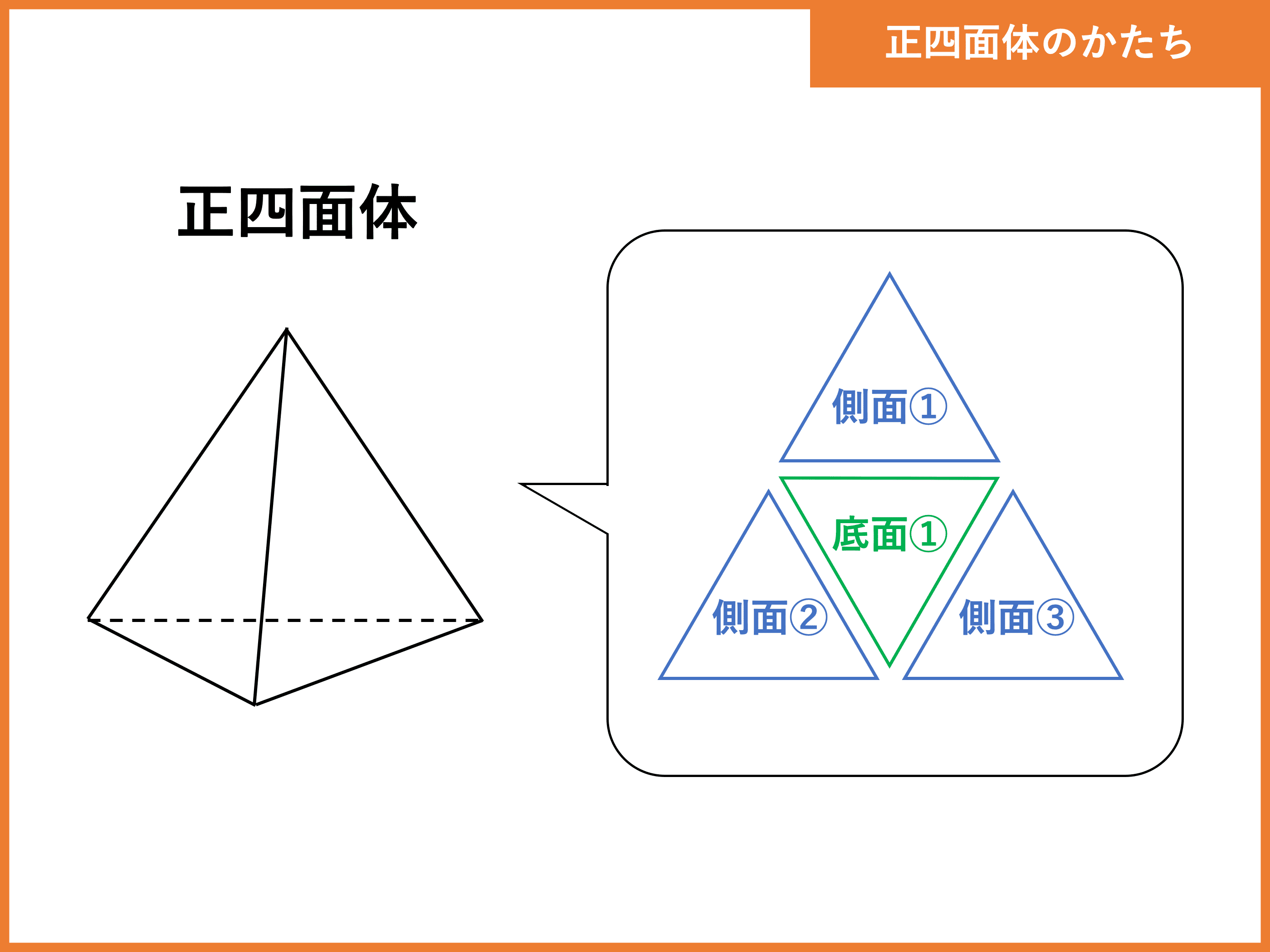



画像をダウンロード 球 展開 図 書き方




19 号 検知装置 Astamuse
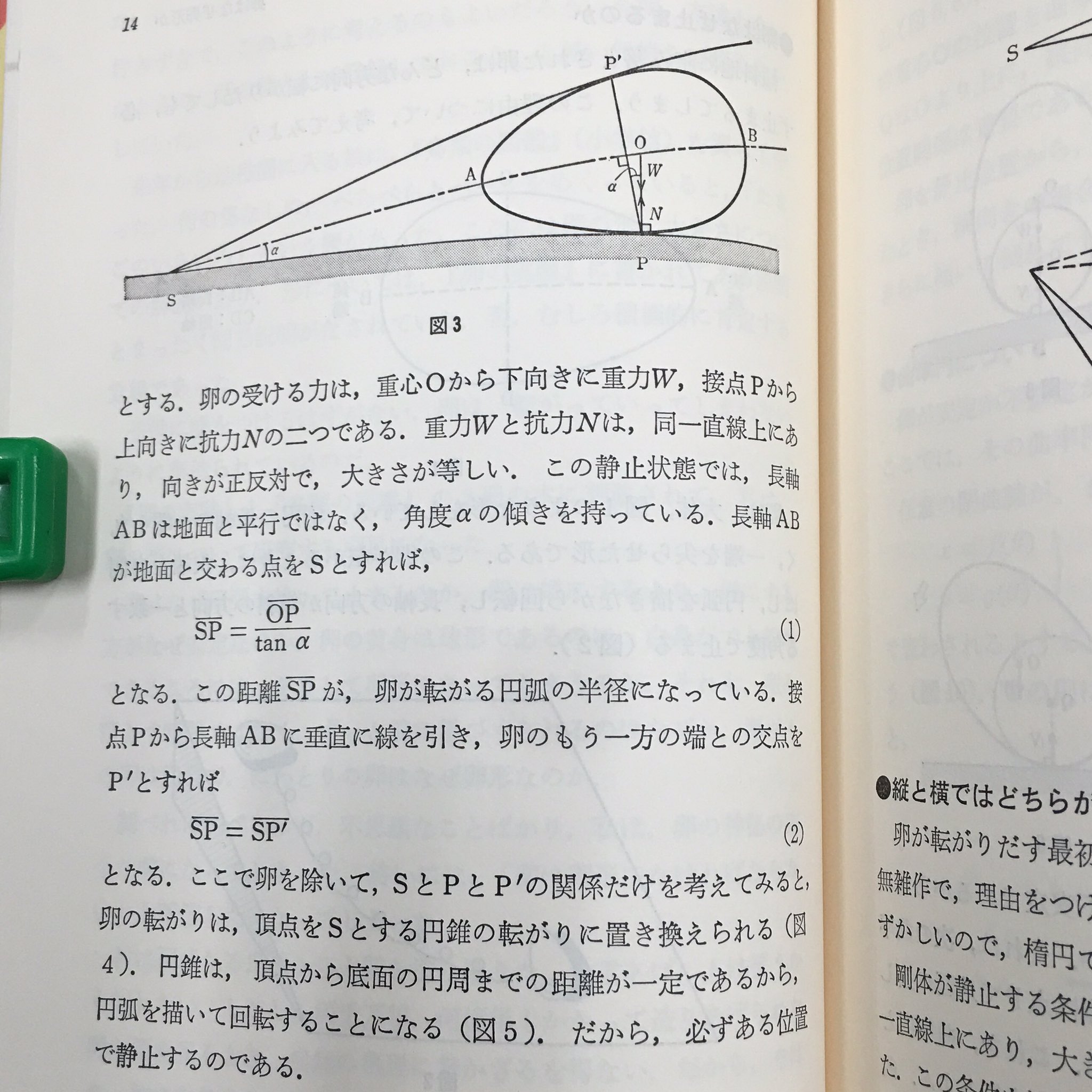



日本評論社 V Twitter 卵はなぜ卵形か より チコちゃんに叱られる で紹介された卵が転がる円弧の半径の式 Sp Op Tana 地面に静止している卵があり重心をoとする このとき楕円の長軸abは地面と平行ではなく角度aの傾きを持つ 長軸abが地面と接する点をsと



2



Misc Mathematics Lecture
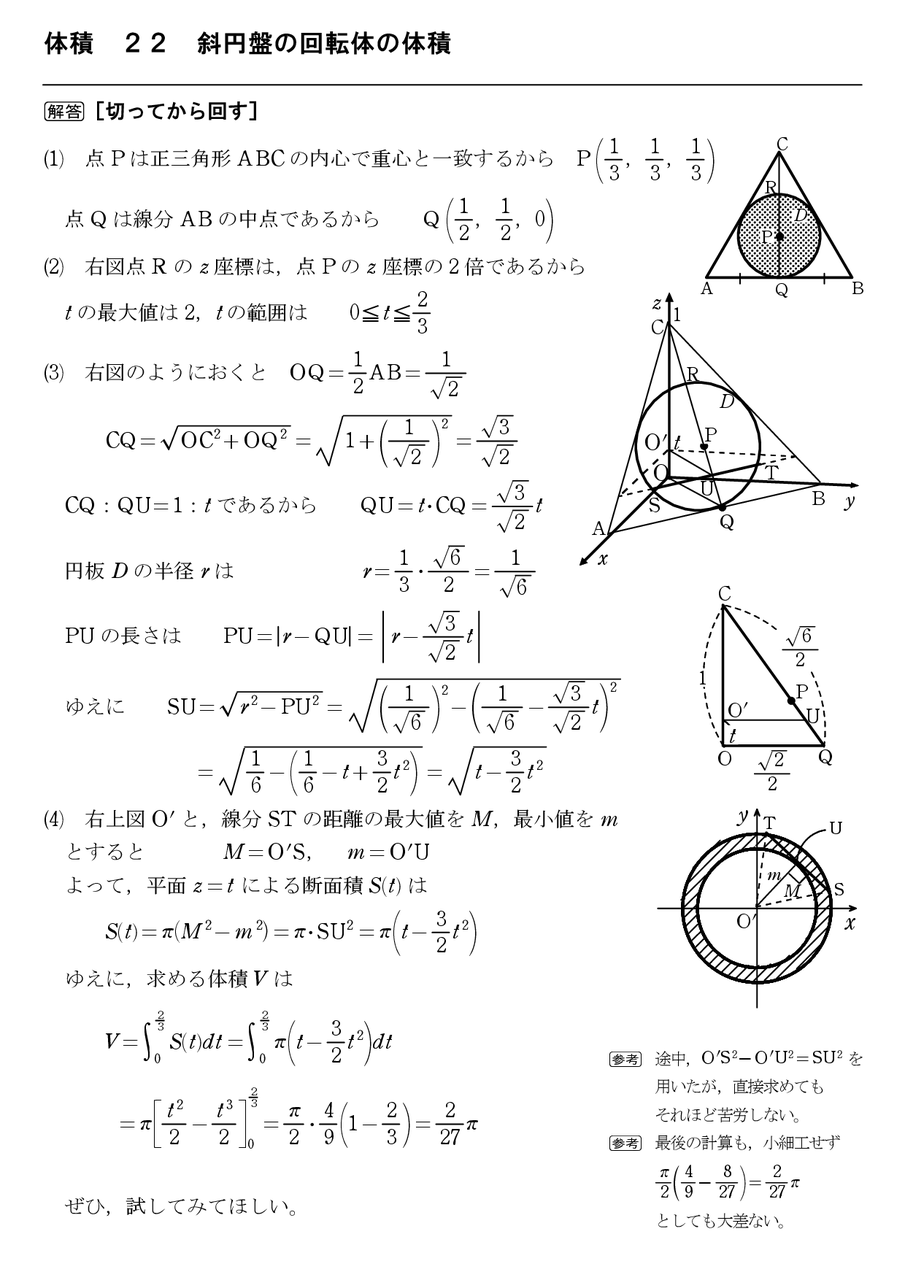



体積 27 円錐の回転体 怜悧玲瓏 高校数学を天空から俯瞰する




1時間連続で点灯 まるでキャンドルな炎を再現 本格スピーカ内蔵の Ledランタンスピーカー でおうち時間を贅沢に Skyward スカイワードプラス



Ipsj Ixsq Nii Ac Jp Ej Action Repository Action Common Download Item Id 1096 Item No 1 Attribute Id 1 File No 1



Freecadの加算パイプの変わった使い方 円錐 正四面体の作成方法 3pysci



Www Tsumugi Ne Jp Member St3 5sidou Pdf



Ppt 第 6 章 真直はりの曲げ応力 Powerpoint Presentation Free Download Id




高校数学 数 100 立体に内接する球 Youtube



Misc Mathematics Lecture



Http Hooktail Sub Jp Mechanics Cg Index Pdf



至急お願いします 合成重心が分かりません どなたか教えてください も Yahoo 知恵袋




Amazon Co Jp 保護用品 プラスチック道の円錐形の折りたたみ望遠鏡のアイスクリームのバケツのroadblockの列の駐車 安全標識 Color Orange サイズ 60cm 産業 研究開発用品




基本 円運動演習1 円錐振り子 Physicmath フィジクマス




21 号 オットマン Astamuse



Www Cosmo Sci Hokudai Ac Jp Ssd Doc Sec02 Section2 Pdf



2



0 件のコメント:
コメントを投稿